Math Made Easy: Problem of the Day 19

Many of my students panic when they see exponential equations. All their knowledge of how exponents work goes out the window the moment you put a little variable up there. They’re not the only ones who do that. For some reason, that little variable in the exponent makes people do crazy things. They start desperately trying to remember their logarithm rules, or they just start making up some of the most bizarre math I’ve ever seen. And as a tutor, I’ve seen plenty of strange stuff. The key for a lot of them, as it is for most math, is to just relax and take in steps, one step at a time. If you can’t remember exactly what to do, do what you CAN do, and if you can’t see the next step, just rewrite things in a different way that means the same thing. Let’s remember that as we do today’s problem.

Here we have the scary exponential equation, with two variables in the exponents. And we’re told to solve for one in terms of the other. That means we basically want to isolate that variable, or get it on its own on one side of the equation, and all the junk on the other side, and then put that junk in the simplest terms we can. Remember, when you’re told to solve or evaluate, you’re not done until your answer is in the simplest possible terms.

The first thing I’m going to do, is move that coefficient. It’s the easiest thing at the moment, so I do it first. Just divide both sides by 4. That at least gets the x term mostly on its own, though it’s still in the exponent. Next, I want everything consistent. I don’t want a combination of fractional and exponential notation unless I can avoid it, or unless it somehow makes me see something I couldn’t see before. Here, it doesn’t help, it just muddies the waters, so I’m going to express that 4 as a negative exponent, bringing it out of the fraction.

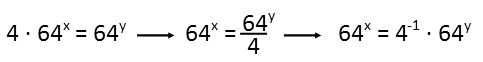
Next, I see that x and y have common bases, but the negative exponent does not – its base is 4. How can I fix that? Well, I recognize that 4 is just the cube root of 64. How convenient! If I change the negative one exponent to negative one-third, I can also change the base from 4 to 64. 4^-1 is the same thing as 64^-⅓ since a fractional exponent just means a root. So I make that change. Now I have all three exponential terms with the same base. I’m heading towards happy land. Now I just apply the multiplication rule for exponents, which requires both terms multiplied to have common bases. It tells me to add the exponents when two exponential terms with common bases are multiplied and combine them into one exponential term. That gives me 64^y-⅓. And just like that, I’m practically finished. Now that I have only one exponential term on each side of the equation, and nothing else, I can easily see that the bases are now essentially something I can ignore, leaving me with the conclusion that x = y – ⅓. And I’m done. x has been expressed in terms of y.

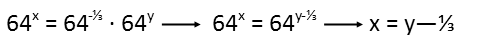
One interesting side note before I go. That exponential equation had a linear solution set, which is pretty nifty. So if you want to test it, remember you *have* to pick points along the line x = y – ⅓. I recommend testing your results. It’s always be good to be sure that the math you worked so hard on didn’t produce gibberish.