Math Made Easy: Problem of the Day 2

Let’s do some Algebra today. We’re going to tackle a problem with two variables. Here’s the problem:

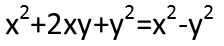
Typically, whenever you have more than one variable, you need at least one equation for every variable in order to obtain a solution. Too few equations, and the system is unsolvable. So for our problem above, we typically need two equations to solve, since it has two variables. Which might make this one seem unsolveable. Or is it?

Another consideration is that we see it involves quadratics. A typical rule for polynomials, is that there exists one possible solution for every degree of the polynomial. The degree is equal to the highest exponent. So, for quadratics, or polynomials of degree two, we see there are 2 possible solutions. Let’s keep that in mind as we attempt to solve this problem.

There are two different approaches to this problem, and I’m going to start with the less obvious one first (and with reason, as we’ll see later on). The very first thing I’m going to do, is I’m going to divide both sides by the entire right side (x²-y²), which effectively gives me a rational expression equaling one.

Next, I recognize two things. First, the numerator, or top of my fraction, is a perfect square, so I’ll factor it as such. Second, the denominator, or bottom of my fraction, is a difference of squares, so I’ll also factor it accordingly.

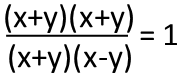
I then see that at least one (x+y) term exists in both the numerator and denominator, so I can cancel one each, leaving us with a much simpler fraction. The quadratic has become linear.

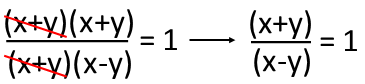
For my next step, I’ll multiply both sides by (x-y), effectively moving it back to the right-hand side of the equation. I’ll then subtract x from both sides, making it go away, leaving me with y=-y. The only way this can be true, is if y=0. So we have one solution for the equation the exists everywhere along the line y=0.

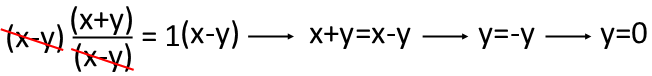
Are we done yet? Let’s take another approach and see. This time, we see that there is a positive x² on both sides of the equation, so it effectively cancels and goes away when we subtract x² from both sides. I’ll then add y² to both sides, moving it to the left side of the equation.

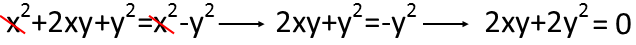
I can now see that I can factor 2y out of all three existing terms, so I’ll do that.

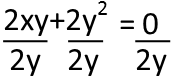
This leaves me with x+y=0, which means we have a solution along the line x=-y. So we have another solution set for the equation. BUT, this means we now also have a unique solution for the equation. Where the two solution sets cross, we have a single point that solves the equation - in the solution set x=-y, where y=0 (as from the first solution set), so does x. So we can say this equation has two solutions sets - y=0 and x=-y, which intersect at the point (0,0).

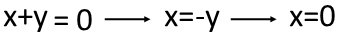
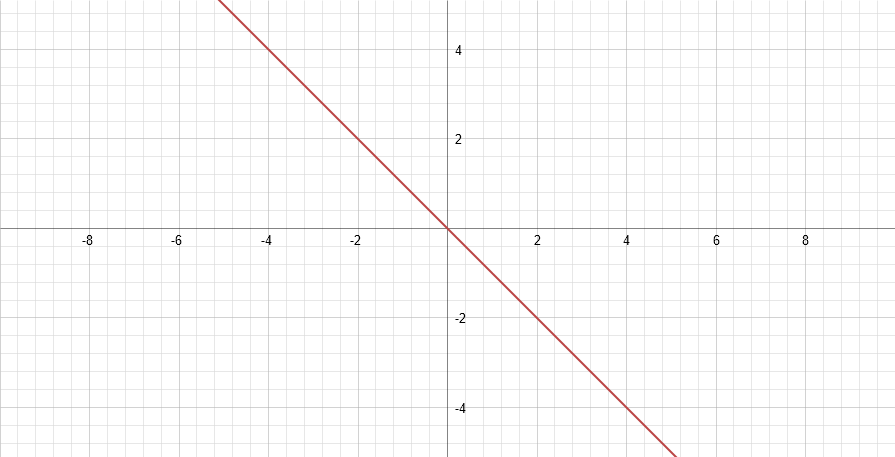
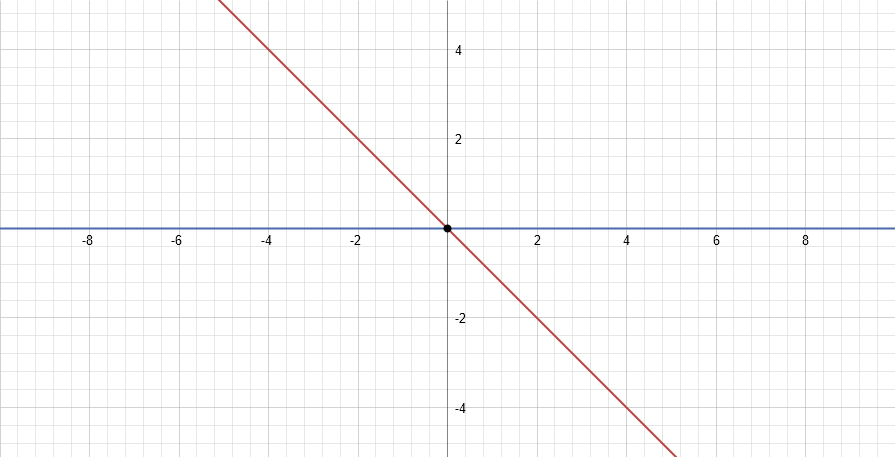
What is our lesson learned from this problem? While there may be multiple ways to approach a mathematical problem, they will not always produce the same solution. This doesn’t make one way wrong. What it means, is that, with more complex situations, we cannot always let ourselves rest when we find a solution after using one technique. We need to check our work, and try other possible methods to see if there indeed IS another solution, especially when we’ve got a system where we know there could be more possible answers (as in this quadratic where we knew from the start there could be two possible answers). In other words, don’t get cocky, or the math could bite you.