Math Made Easy: Problem of the Day 20

We haven’t covered any sequences yet, so let’s do one for today. Can you find the 100th term in this sequence without using a calculator? It’s quite doable!

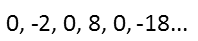
So how are we going to solve this one? When solving sequences, we need to think of each term in the sequences as generated by a function, where we start with the variable n representing the place the term has in the sequence (in other words, for the first term, we replace all the n’s with 1, the second term we replace them all with 2, etc.). Then we look for patterns, and start trying to figure out how we can manipulate that n to achieve the pattern we see. So let’s examine this sequence’s pattern.

The pattern might not be all that clear, other than the fact that every other term is a zero. That’s our first clue, and important one. The next big clue as to one of the functions involved in this sequence is the fact that the sign changes on all the non-zero numbers. First negative, then positive, then negative again. This fluctuation between negative, zero, and non-zero numbers tells us we have either a sine or cosine function involved. The fact that the series always produces an integer tell me that, inside the cosine or sine function, the n is multiplied by π, and perhaps something else. So let’s picture our unit circle, and see where things come out zero, and where they come up either positive or negative. For the cosine, it starts at positive 1, then goes to zero, then negative one, then zero. But our function starts at zero. That’s more like sine. Okay, the sine starts at 0, goes positive, then zero, then negative. That’s not our function either. But if we have nπ inside the cosine, we’d have negative, positive, negative, positive. You’d never get zero with that because you’d just be flipping backing and forth between the x=0 and x=π positions on the unit circle, which would just alternate ouptuts of 1 and -1. So that’s not quite what we want. Inside the sine, we’d have zero, zero, zero, zero. You’d never get a result other than zero with multiples of pi inside the sine function for the same reason the cosine function alternates, only here our output would always be zero. So we must be multiplying by some fraction of π. π/2 inside the sine would give us 0, -1, 0, 1. Hey, that looks right as far as the pattern of the sign in our sequence. It looks like we have part of our function. But we’re not done yet.

Now that we have a way to alternate the sign as well as those zero return values, we tackle the rest of the sequence function. It doesn’t look like anything is being added, or we’d never see those zeros in the sequence. So there must be a multiple. They’re all even, but then, if we look at their positions, those are all even, too, so that might not be a lot of help. Okay, ignoring the sign (since we’ve already figured out that’s a result of the cosine function), we can try looking at the proportions of the terms. I don’t care about the difference because I’ve already ruled out a linear progression (adding something). So, 8 divided by 2 is 4. But 18 divided by 8 is not 4. We don’t have a simple geometric progression here. We must have an exponential progression, and because it’s not obvious, I think we ALSO have a geometric progress (in other words, an exponent AND a multiple). Let’s test that. In the second position, if we square 2 we get 4. For the 4th position, 4 squared is 16. And in that 6th position, 6 squared is 36. One quick look at the sequence, compared to those, I can see that each of those results has been halved. And I’ve found my sequential function! It looks like this:

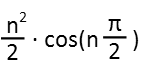
So now to figure out the 100th term. And remember, we’re NOT using a calculator. I plug in 100 for n, and, I see that, for the cosine function, I’ll have 50π on the inside, which is an even multiple of pie. All even multiples of pie will return you to the starting position on the unit circle, which means the cosine here just returns positive one. So all I care about is 100²/2. That’s a 1 with 4 zeroes (two zeroes in one hundred twice, so 4 zeros), divided by 2. Quickly done without a calculator, I divide the first 10 in that number by 2, which is 5, and I have 3 zeroes left on the end. So, 5,000 is our 100th term.

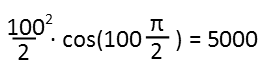
Figuring out sequences can be fun! They just require a bit of logic, and a familiarity with mathematical functions. They can be a real test of your math skills, since solving them really does need you to be able to remember everything you’ve been taught about mathematics. Little puzzles, they are, waiting to be cracked open and put back together.