Math Made Easy: Problem of the Day 21

On the SAT, they love doing problems that try to catch students who go on math autopilot. They’re not really trying to test your math skills, so much as they want to test your critical thinking skills. One way they do this is with problems involving arithmetic means (or averages), and problems with consecutive numbers. For many students, seeing that problem involving consecutive numbers on the SAT is the first time they ever have to constrain their math to consecutive numbers beyond just figuring out sequences, and it throws them for a loop. So let’s do a similar problem for today.

The arithmetic mean of five consecutive even numbers is 42. What are the five numbers?

To solve this, let’s first consider the relationship of the five consecutive numbers. We will name the first one n. Since even numbers are always two apart, the second one is n+2, the third n+4, the fourth n+6, and the fifth n+8. Their mean we find by adding them all together and dividing by 5. So I can write the equation:

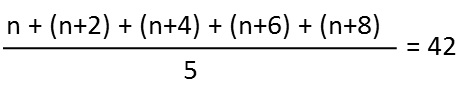
Now we just solve. First, let’s add up all those n’s and the constants in the numerator.

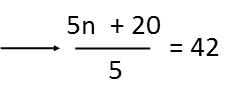
Simplify the fraction. I see that 5 is a factor of both terms of the numerator, so I can cancel by 5s.

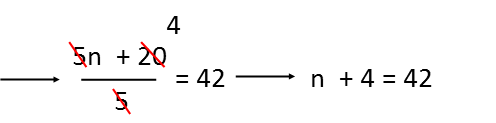
Subtract 4 from both sides to move the constant.

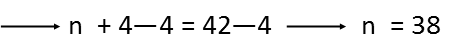
We now know the first term of the set. So the whole set is just 38, 40, 42, 44, 46. That’s one way to attack this problem. Unfortunately, it’s also the slow way, and that’s what they’re counting on in the SAT. The problem is designed to make you go on math autopilot and waste time, when you could have used your critical reasoning to solve it faster. Now let’s do it the fast way, with reason, and less computation.

Since they’re consecutive numbers with an average of 42, we know that 42 is CENTERED in the set. It’s not just the average, it’s the median, as well, a property of consecutive numbers and the fact that there was an odd number of them (if we had an even number of them, the average would have been odd and not part of the set). They’re even, which means 42 is actually a PART of the set. It has to be the third number. And since I know that consecutive numbers are always two apart, and there are two numbers before the third number, I just subtract 4 from it (2 times two since there are two numbers to the left of it), and I arrive at 38. Or I could just count backwards by twos, whichever I find faster. So, again I arrive at the set being 38, 40, 42, 44, 46. This way is actually a LOT faster than the equation and calculation route.

The lesson for today? Remember that, when doing math, you have your reason to aid you. You don’t always have to set up equations.