Math Made Easy: Problem of the Day 22

Another way the crafters of the SAT like to test your critical thinking faculties is to present a problem where you have to devise a number. It will be made of a certain number of digits, and they’ll lay out some rules for you to figure out each digit. Let’s look at one like that today.

This problem might seem a nightmare, but it should be doable. The best way to do this, is assign a variable to ONE of the digits. Then try to use the rules to express each other digit in terms of that variable. So I’ll go ahead and assign the variable x to the first digit. If I reach a point I can’t think of how to exactly express one of the digits in terms of just x, I’ll assign it a new variable, and try to write equations for it. Doing that, we get the digits, in order:

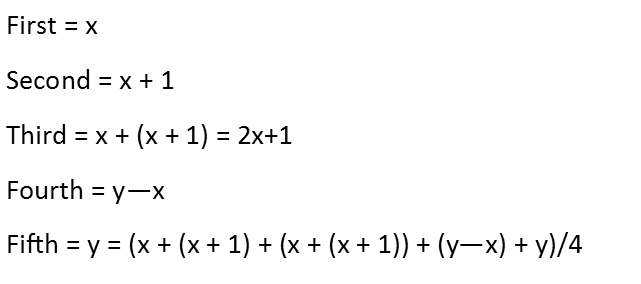
Since the second is larger than the first by one, it is x + 1. The third, since it is the sum of the first and second, we just add our expressions for digits one and two. Note that the fourth and fifth include the fifth in their definitions – I need a variable for it, so I’ll call it y. That means the fourth digit is y-x, and the fifth is the more complicated sum of all fives digits, including itself, all divided by four. So how am I going to solve this? I could try the plug and play method, where I just plug in numbers until I find ones that work. But let me try to simplify that fifth one first, since I actually have an equation there. So I’ll do so by adding all the x’s, constants, and y’s and see what I have. I then solve for y to get it further simplified.

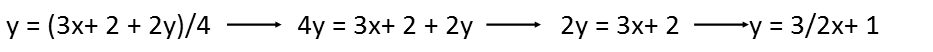
Now that that’s simplified, I have to apply my reason to this. I only have one actual equation, but two variables, so I can’t use a system of equations to solve. My reason is the only thing that will help me now. So let’s examine each digit in turn, starting with the fifth.

We know the fifth digit CANNOT be zero. If it is, we end up with the fourth being less than zero. So that doesn’t work. FURTHER, we know it must be greater than one, since it is included in its own sum, and the second and third are sums of sums. And looking at the equation for y, I see the first digit HAS to be an even number to produce an integer value for y. From the expression for the third digit, I also see that the first digit cannot be greater than 4, as any other even number used in that expression produces a number bigger than 10, which is not a single digit. So I only have to test the numbers 2 and 4 for the first digit. Let’s test two first. For that, we’d get 235 for the first three digits. Plugging 2 into the equation for the fifth digit, we’d get 4. Our number would then be 23424. But this repeats digits, so this can’t be our number. So the first digit has to be 4. Applying the rules, we get 45937 as our five digit number. All five digits are unique, and they all meet the rules as given.
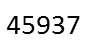