Math Made Easy: Problem of the Day 23

Sometimes even the best of us fall into the math autopilot trap. Here’s an example of a problem that tricked me into starting to go about it the long way:

So, when I was with my student, I readily recognized the first thing needed to do this: one doesn’t need knowledge of conics to solve this. But I still started going about it the long way. My student was struggling, as she didn’t make the first couple connections needed, but after I helped her see those, and I was half-way through doing it the long way, she had a light-bulb moment, realized what the short way was, and did it before I got through the next step of the method I was showing her. She was correct, and I had my moment of embarrassment for failing to take my own advice of not going into math autopilot and spending a few moments to think of the shortest way to do it.

So how DO we do this the shortest way? The first thing we need to recognize, is the situation described forms two triangles – I’ve illustrated them below, with the big one being outlined in bold lines, and the smaller one is shaded in pale blue.

We recognize that the vertical leg of that small triangle is just 12 – 4 = 8 units. We can calculate the radius of the big triangle from the area of the base of the big cone, which is just a circle. So we remember that the formula for the area of a circle is simply π times the radius squared, we solve for r, the radius, and we find that it is 6, as I’ve labeled in the diagram.

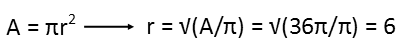
Here’s where I went astray. I knew I could calculate the vertex angle of the triangle using the unit circle. From that we could then calculate all the legs of the small triangle, and from there the area of the small base circle. But that’s absolutely the long way, especially since, for her problem, it produced some really ugly numbers in the middle that were difficult to work with. Instead, what I should have done, and what she did, was recognize that we have two similar triangles. Which means we can use simple proportions to solve the problem.

So we set up the proportions – one fraction equals another. We put x on the top of one to represent the radius we want to find. On the bottom, we put the radius of the big circle, which we know. For the other fraction, we put the length of the vertical leg of the small triangle, which we know, and on the bottom, the length of the vertical leg of the big triangle. We then solve. Instead of cross-multiplying, which is hammered into people in elementary school, and actually makes you do more work than you need to do, just multiply both sides by six, effectively moving the six to the right-hand side of the equation and isolating the variable, as we want to do. Then just simplify the result. I did that here, and it turns out the radius of our smaller circle is 4.

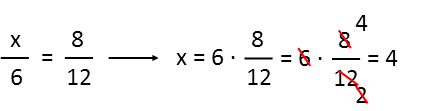
We now plug that in to the formula for the area of a circle, and just like that, we’re done. The area of the smaller circle is 16π. It didn’t really take even a minute to do this the fast way. Lesson learned: Once again, don’t go on math autopilot. Even the best of us can do it, and it can trap you into doing a LOT more work than you need to do.
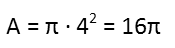