Math Made Easy: Problem of the Day 25

Today’s problem is all about pattern recognition. Let's examine the following question:

That’s a huge number! Even with a calculator, this problem presents a difficulty. The majority of calculators can’t even compute it to begin with, and those that can aren’t capable of displaying all 904 digits that comprise it. Even Google Calculator has problems with it, thinking the number is so big it must be infinite (seriously, put it into Google Calculator and see what happens). Wolfram is able to compute it (it’s 1.23 x 10⁹⁰³, and even able to display all the digits, but that’s cheating, and there’s actually a very fast way to figure out the last digit.

Here’s what you do: create a table of the values of exponents of 8, starting at 8¹. Keep going until you see the pattern. Here’s my table going through 8⁸.

Note that the last digit repeats in cycles of 4. That means that every time you hit an exponent that is one higher than being divisible by four (like 5), the cycle starts over. So, first I want to know how many cycles we go through with 8¹⁰⁰⁰. Just divide 1000 by 4, and it comes out to an even 250 cycles.

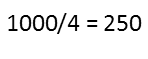
Which means it just ended a cycle, so I look at the last digit of the last number of the cycle (8⁴), and I see it is a 6. So 8¹⁰⁰⁰ must end in a 6. If I wanted to know the last digit of 8¹⁰⁰³, I just go 3 more steps in the cycle, so it has the same last digit as 8³, which is a 2.

Another trick for our math toolbox! Using patterns to help us figure out our problem can save the day sometimes, just like some of our other simple tricks.