Math Made Easy: Problem of the Day 26

In Star Wars: The Force Awakens, Starkiller base literally absorbs a star to power a superweapon. Now we all know the Star Wars movies require a substantial suspension of disbelief to be enjoyable (and they certainly are wonderful when taken as science fantasy), but for a moment, let’s unsuspend our disbelief and examine this scenario. Just how much would it increase the gravitic pull on the surface of the planet? So here’s today’s problem:

There are two ways to solve this problem. I’ll do the harder one first, then the easier one. As I do this, remember weight is a force – the attraction of your mass to the Earth’s (or whatever body you’re standing on). In metric, weight is measured in Newtons. In Imperial, pounds serves for weight (part of why the imperial system is so bad – it tries to make pounds serve for both mass and weight, when the two are completely different properties).

To do this the longer, harder way, we must use the the formula for gravitic force felt between two masses (where G represents the universal gravitational constant, m₁ and m₂ the two masses, and d the distance between the two objects centers of mass):

G is a known quantity, and is 6.673x10^-11Nm²/kg²

Let’s define m₁ as the mass of the star. One solar mass is 1.989x10³⁰kg. We actually aren’t even going to add in the mass of the earth, as it is 6 orders of magnitude small than that of the sun. Which means in that scientific notation, its first digit doesn’t even show up for 3 more digits. It’s negligible.

That leaves m₂ as the mass of the person: 100kg. And the distance is the radius of the earth (the distance from the Earth’s center of mass to yours is essentially one earth radius): 6.371x10⁶ meters.

Note I’m working in meters and kg to stay consistent with the units of the universal gravitational constant. Also note that all units cancel except Newtons when we do this.

So let’s just plug all of those in, and we get 3.270x10⁸ Newtons:

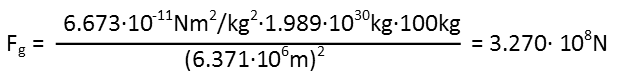
That’s not very intuitive, at least not for Americans. Since we’re used to working in pounds, and even in metric countries, we’re used to saying we “weigh” so-and-so many kilograms, what does that really mean? Well, let’s divide it by the acceleration due to gravity at one earth mass. This will yield an answer in effective kilograms, which will give us a better idea of how much the person’s weight has increased: It’s still in the order of magnitude of 10⁷, which means he weighs over 3x10⁵ times as much. That’s three hundred thousand times more weight. I certainly doubt anyone would be able to stand on the surface of Starkiller Base after the star was absorbed if we didn’t suspend our disbelief so we can enjoy the fantasy of the movie. Thank goodness we do.

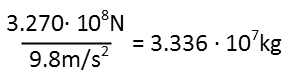
Now that we’ve done it that way, let’s do the easier way. Just as the Earth’s mass is insignificant to the Sun’s, so yours is to the Earth’s. By orders of magnitude, it doesn’t even begin to compare. So when we use that formula for gravitational force, your mass practically doesn’t even effect it, and the difference between your mass and another’s doesn’t effect it either. That’s why your teachers confidently use the same figure for acceleration due to gravity on Earth’s surface for pretty much everything, regardless of how much its mass is. So, knowing that, let’s use a different formula for force, and just compare the suns mass to the Earth’s. Well, the sun is 332,946 times the mass of the earth. That’s 3.329x10⁵. If we multiply that by the 9.8m/s² figure we use for the acceleration due to gravity on the earth’s surface, we have the new acceleration due to gravity. Now we can just use good ol’ Newton’s Second Law to calculate the fellow’s weight after Starkiller Base has absorbed the star:

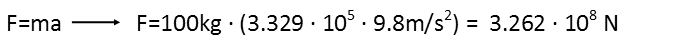
And lo and behold, we get essentially the same thing we did before. In fact, it’s the difference in the mass of the Earth and Sun that is the difference in the poor individual’s weight. So we didn’t have to do much calculation to begin with. But, thank goodness Star Wars is fantasy, and we really don’t have to worry about scientific accuracy to enjoy it. Because, man, was that freaking cool to see a star getting sucked into a giant planetary vacuum cleaner.