Math Made Easy: Problem of the Day 27

Another thought I’ve recently had about Star Wars, is wondering just how much power would a lightsaber pack, assuming we could make one, and the blade really is just made up of photons that are somehow constrained to zoom back and forth between an endpoint and the hilt. So, to that effect:

For this problem, since I can’t find anywhere online where anyone’s actually measured the luminosity of lightsaber from the films, note that I ask we only calculate how much power one photon will impart. So, let’s calculate the luminous flux of that photon at any given point on the blade. We’re also going to assume that, as in the movies, nothing stops these photons – they zip right through whatever solid object they encounter, somehow imparting all their energy without also losing it along the way, and so continue along back and forth between the tip of the blade 1 meter away.

First, we need to calculate how many oscillations the photon makes – in other words, how many back and forth trips. That’s easy enough – we just divide the speed of light by the distance the photon travels, which is 2 meters (to the tip one meter away and back to the hilt). We see that the photon makes 1.5x10⁸ oscillations per second.

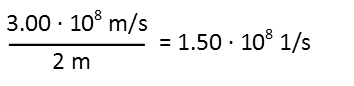
But we also need to recognize that, except at the tip of the blade, any given point will see the photon twice during its trip. So we need to double that figure for how many times a photon passes a given point excepting the very tip. So the actual flux of photons (note I’m careful not to use radiant flux or luminous flux here, because those are not measured in photons) of any given point along the blade (or path of the photon) is going to be 3.0x10⁸ photons/second (even though it’s the same photon, the point sees it 300 million times in a second, so it is the same thing as if 300 million photons passed through that point in a second).

How much energy is being imparted to that point? Well, we can calculate the energy of any given photon if we know its frequency:

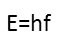
h is just Planck’s Constant: 6.626x10^-34m²kg/s; c is the speed of light; and the photon’s frequency is easily found from the wavelength:

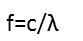
Plugging that in for frequency, we get:

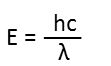
Assume this is Luke’s lightsaber we’re talking about. Blue light has a wavelength range of 450-495nm. Let’s put his square in the middle of that (because it’s not very green or very purple) at 475nm. Convert that to meters and plug everything in to find how much energy each photon has:

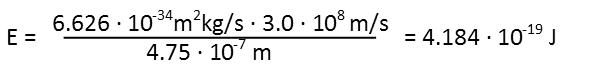
That’s not very much. But multiply that by how many times per second that photon passes any single point, and we get:

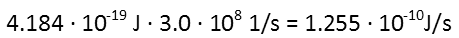
Note that 1 J/s is 1 Watt or power. This still doesn’t seem like much. But this is EVERY SINGLE POINT on the photon’s path. So it’s cumulative. So if we assume that each atom in its path is that single point, each atom in its path is being hit by 1.255x10^-10 Watts. Is that enough to cut through metal like they do in the movies? Well, let’s look at the ionization energy of Titanium. That’s the energy needed to strip an electron. Titanium’s ionization energy for its innermost orbital (in other words, the energy we need to apply to strip ALL its electrons) is 4966 eV. With atoms we tend to measure energies in electron volts instead of Joules, so let’s convert that to Joules to compare it to the energy of our single-photon lightsaber. That’s 7.956x10^-16 Joules. So every second, our single photon blade is bombarding every single atom in its path with 1 million times the energy it needs strip all the electrons from a Titanium atom. That would more than melt the Titanium. It would convert it to plasma.

Now, before you say “Evan, a single photon can’t impart more energy than it carries itself – that violates the laws of thermodynamics.” Yes, we know that. This is Star Wars. Everything about these movies violates the laws of physics. The whole concept of the lightsaber does, which is why we suspend our disbelief in order to enjoy the movies.