Math Made Easy: Problem of the Day 28

Always remember there are frequently multiple ways to approach math problems. Treat it as a toolbox, and always pick the way that works best for you. For today’s problem, I’ll present two ways to do it, and you can decide which way you think is easier.

First, I’ll do the way I think takes a bit longer. From this problem, we can write two algebraic expressions – the first recognizing that if you assign the variables x and y to how long it took Peter and Marco to get to work, respectively, you can write an expression equating their distance travelled by multiplying their speeds:

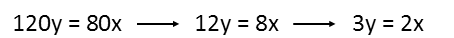
The second equation recognizes that the sum of their times travelled, in minutes, equals an hour. I then solve it for x in terms of y:

And then plug that into x in the first equation, then solve (note that I consistently keep everything in fractions as long as I can, and I *always* simplify before I multiply - saves a lot of headache):

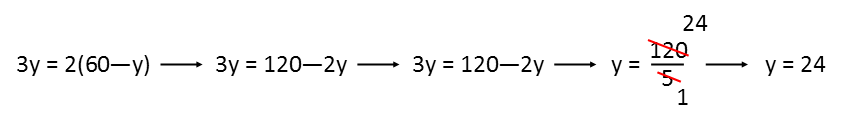
Which tells us that Marco took 24 minutes to get to work. We can also find out how long Peter took to get to work by plugging in 24 for y in the original equation:

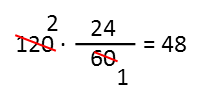
And now that we know it took Marco 24 minutes to get to work, I put that over 60 (for the number of minutes in an hour), and multiply by the 120 kilometers per hour speed, and we arrive at 48 kilometers being the distance he travelled to get to work. I don’t need to do the same for Peter since they went the same distance, but you might want to do so just as a check.

So now a second way to do it. If we set this up as a proportion problem, we see that the ratio of their speeds is simply 80/120, which we can simplify to 2/3.

When dealing with proportions, recognize that the initial ratio you get between two parts of a whole is NOT the fraction you want to multiply by. The fraction you use will have a denominator that represents your whole. Here, the whole is made up of 2 parts plus 3 parts, for 5 total parts. So the smaller thing (the least time) is 2/5^ths of the whole, and the larger 3/5^ths. Since Marco took the least time, we will just multiply 120 times 2/5 to find out how far he went. We get the same result as before: 48 kilometers.

I personally think that, for this problem, the proportions method is faster and easier. It’s a bit less work as long as you’re able to remember how to get the proportion, and then don’t forget the whole is made up of the parts. But the important thing is that you master all the methods so that when you see a problem, you can pick which one works best for you.