Math Made Easy: Problem of the Day 3

Today’s problem comes from a physical situation I’ve been examining. In it, I ended up with an odd looking fractional expression, which I needed to simplify to determine if I’d gotten my units correct. Here it is:

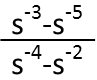
I have to admit, when I first looked got it down to this, I stared at it for quite some time trying to determine what my next step would be. How could I make sense of this? Then it hit me. First, I need to remember that negative exponents follow the same rule as positive exponents, so I should let the negative exponents throw me. Second, how could I break these apart? I see a difference of squares in the numerator. Can I take advantage of that? Absolutely. In order to do so, my first step is to factor an s^-1 out of both terms on the top. And since that’s just 1/s, I’m going to go ahead and move it to the denominator while I’m at it.

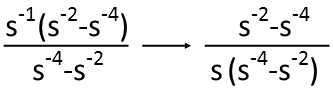
Now that I’ve done that, I have a difference of squares in both the top and bottom. Just because the exponents are negative, and that the powers are two and 4 in both, doesn’t mean it doesn’t work the same. It does. So let’s factor both.

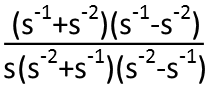
Now that we’ve done that, we can see that we have a like term in both the numerator and denominator. Yes, the powers are in different order, but because both those terms are addition of positive values, their order doesn’t matter. They’re the same term. So we’ll cancel one in top and bottom.

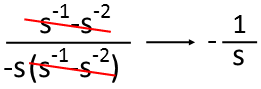
Now I’m going to try to get the remaining terms to look the same. To do that, I’m going to factor a negative sign (-1, effectively) out of the parenthetical in the denominator, giving me a negative s^-2 and positive s^-1, just like in the numerator. I can reorder those accordingly.

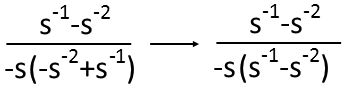
Now I can cancel those remaining two like terms in the numerator and denominator, leaving me with the simplest form of the fraction. Which turns out to be the kind of units I wanted, by the way! And who would have thought upon initial inspection of the fraction that we would have gotten something so simple! This problem was entirely about two things. Don’t let negative exponents throw you – they work the same as positive exponents, as far as the algebra’s concerned. And recognize those difference of squares when they’re present, and take advantage of them to help you find ways to simplify your situation.