Math Made Easy: Problem of the Day 30

Geometry problems are always good for demonstrating math’s applicability to the real world. To that end, let’s look at this problem today, which could very well appear on an SAT.

The first key to working this problem, is visualizing what’s going on. To do that, we can’t let our mind get stuck in the wrong mindset – sometimes, when a student sees the phrase “1 cubic measure of” something, they immediately visualize a cube, and with a problem like this, that can shoot you in the foot. So what we need to picture instead, is that, since the tank is a cylinder, and its water level lowered, effectively a cylinder of water was removed. This would be like if there was another tank of the same radius catching the water leak, like in the picture below.

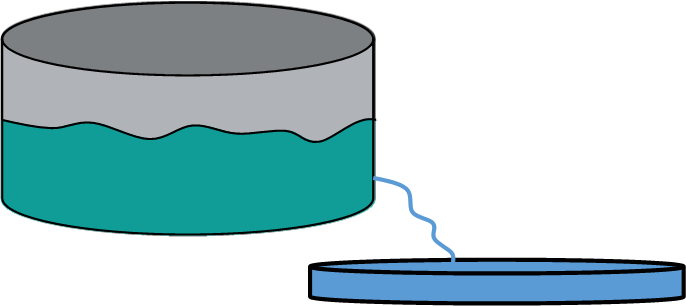
So we know the cylinder of water removed has the same radius as the tank it’s in – fluids take on the shape and dimensions of their container. Since we need to know the radius of the tank, all we have to do is calculate the radius of the cylinder of water removed. So we remind ourselves of the formula for the volume of a cylinder, and solve for the radius, like so:

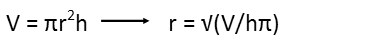
Now we can plug in our values. Since the water level lowered by centimeters, we need to convert that cubic meter to centimeters. Recognizing that 1 cubic meter is made up of 100cm x 100cm x 100cm, I’ll express it as (100cm)³. I have a hunch doing so will actually make my problem easier rather than multiplying it out to represent it as 1,000,000 cm, or 1x10⁶cm.

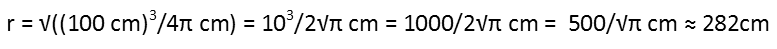
And it does. I’m able to take advantage of the fact that 100 is a perfect square, so I just take the square root of that before I cube it. Now I’m only cubing 10. I also take the square root of 4 while I’m at it. Next I go ahead and cube 10. Then, finally, I simplify my fraction, and then rationalize it since we can’t have radicals in the denominator. For precision, it’s best to leave it in that form, but to get a feel for about what that is, we can evaluate the fraction and see it’s about 282cm.

One last note: If this is on an SAT, check the form the problems are in before you rationalize. Frequently, on the SAT, the answers are not rationalized. So don’t do work you don’t need to do.