Math Made Easy: Problem of the Day 31

Today we’ll do a probability problem with a twist. Usually, when we’re given questions about probability, we know the conditions, in other words, how many of everything involved, and we’re asked to calculate the possibility of the outcomes. But what if we don’t know how many things are involved? What If we know the probabilities, and want to know how many things there were? For instance:

Let’s look at what we know and don’t know first. We know how many black shirts there are. We don’t know how many red shirts, or the total number of shirts. So let’s give the total number of shirts the variable n. That means we have n – 15 red shirts. We know the outcome of two consecutive events is 50%, but to do our math, let’s represent that as the fraction ½.

Now let’s consider those two consecutive events – drawing two black shirts in a row. We can see that those events are dependent, because the first event effects the second. There are both fewer black shirts and fewer total shirts in the bag after the first pull. So we have only 14 black shirts in the bag, and n – 1 total shirts. To calculate the probability of two consecutive events, we represent the probability of one as fraction, here, black shirts over total number of shirts, and multiply it by the probability of the other, as a fraction. Since we know the probability, we can write the following expression:

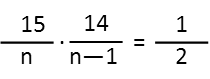
Now we just solve for n. First, since I’m solving for n, I don’t want it on the bottom of a fraction, so I’m just going to conveniently take the reciprocal of both sides of the equation to put it on top. Then I’ll multiply both sides by 15 and 14 to move them to the right side of the equation.

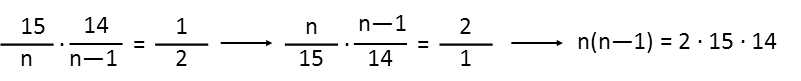
Now that I’ve done that and multiplied the constants, I can see that I have a quadratic equation, so I’m going to subtract the constant from both sides to put this in a form where I can factor the quadratic. I factor the constant by pairs so I can look at all my possible factors, and I see that the only way I can produce -1 (the coefficient of the singular n term in the quadratic) is adding -21 and 20. So I have my factors. This means that n is either 21 or -20 (since the zero, or answer, for each factor is opposite the sign showing in the factor).

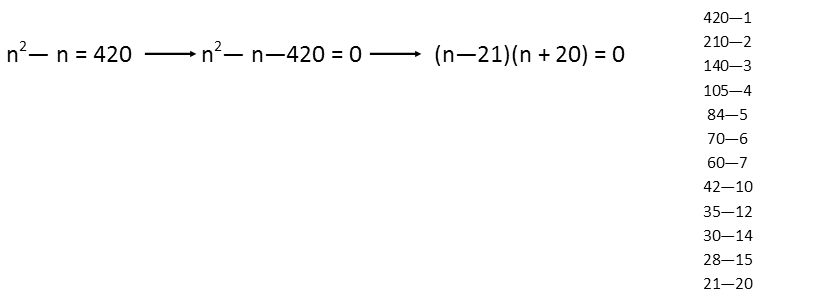
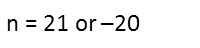
Since I clearly can’t have a negative number of shirts, I know there are 21 shirts in the bag.

Therefor, 21-15=6, so there are 6 red shirts in the bag.

If I wanted to calculate the odds of pulling a red shirt on any draw, I’d just put 6/21, which reduces to 2/7, so there’s about a 29% chance of pulling a red shirt on the first draw.

The only reason a problem like this can appear hard, is because it’s not exactly written in the way such problems are usually practiced. But, the math is exactly the same. By the time you’re doing this kind of probability, you already have the algebra to solve it. So the key here is, just because a problem doesn’t look like something you can do doesn’t mean it is not. Step back and ask yourself, have I done this type of problem, but from a different direction? If you have, then just work backwards, use your knowledge of what you *have* done to arrive at a way to achieve your answer.