Math Made Easy: Problem of the Day 32

Do not cross multiply. Ever. I know just about every American student is taught early on in Elementary school, and has it reinforced throughout their academic career, that cross multiplying is the thing to do. You’re taught it’s easy and is a go-to method. But the fact of the matter is, it causes you to develop bad habits and actually incurs more work for you than you need to do. Today’s problem is a great example of that. Can you solve the following equation for x?

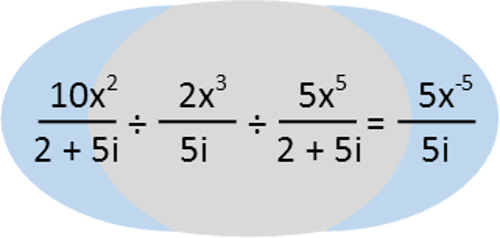
We’re usually taught to cross multiply when we divide fractions. BAD! In this problem, if you try to do that, you’re going to turn it into an absolute nightmare. You’ll end up with our variable x being multiplied by i, and mixed into complex numbers, and you’ll have a heck of a time undoing it. And that’s the exact problem with cross-multiplying. It forces you to do a step that you’re just going to have to UNDO over the course of the problem. Why the heck do we want to do work we’re just going to have to undo? That makes no sense!

So what DO we do here? The best thing, whenever you see division of fractions, is to turn it into a multiplication problem. We remember that dividing by something is the same thing as multiplying by its reciprocal. This should be an absolute mantra in math. Say it again: “DIVIDING BY SOMETHING IS THE SAME AS MULTIPLYING BY ITS RECIPROCAL.” So, starting from left to right, as we do in our order of operations, let’s replace each of those division operators with multiplication operators, and flip the fraction to each symbol’s RIGHT. The very first one to the left is unaffected (while operators work on the object to their left, we still read what it is telling us to do: “Divide this number to the left BY the number on the right,” so it’s the number on the right we need to reciprocate).

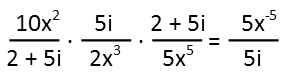
Now that we’ve done that, we can clearly see that we have a few things we can cancel. On the left-hand side of the equation, that complex number is now appearing once in the denominator, and once in the numerator, so I can just cancel it right out. *Poof* it’s gone. No need to multiply it by the 2x³ term ever (we’d have had to do that TWICE if we tried cross-multiplying). I also see I that I have 2x5=10 in the denominator, and a 10 in the numerator, so I’ll cancel those coefficients.

After combining the fractions on the left-hand side of the equation to simplify it a bit, I’ll go ahead and apply the quotient rule of exponents to simplify further – we subtract the bottom exponent from the top. That gives us an exponent of -6, and I know that is just the same thing as a positive exponent, but in the denominator, so I’m going to put the variable in the denominator here (I’m planning ahead, and you’ll see why I did that in a moment).

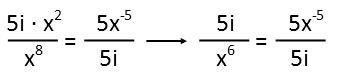
Now I’ll multiply both sides of the equation by the denominators simultaneously – this’ll have the effect of moving all the x’s to the right-side of the equation while moving the imaginary terms all to the left side of the equation, moving me towards what I want to do. I evaluate the new terms, using the product rule of exponents to add them on the right. I also recognize that i² is just -1. And the last thing I have to do is divide both sides by five to make the x term singular. And we’ve solve our equation. x = -5.

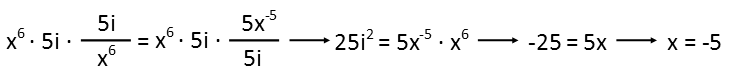
Note we did not cross multiply ONCE. Not across the dividing operator, or across the equals symbol. At the very last step, we COULD have cross-multiplied to achieve the same result, but it’s better to think of it the way I did it: you want to think of MOVING things around, and imagine what you need to do to move them. In that last step, we need to multiply things. There’ll be cases where you only need to move one of the denominators (like in x/5 = 3/5) – if you move both, you’ll end up having to move one right back where it was. So break that cross-multiplying habit, and instead remember the mantra “Dividing by something is the same as multiplying by its reciprocal” when you’re dividing fractions, and think of moving things around the equation when you’ve got fractions facing each other across an equals symbol.