Math Made Easy: Problem of the Day 35

Today’s problem is a geometry problem. It also requires you to use your reason to make sure you’re not jumping to a false conclusion. So make sure you draw pictures and think it through before you go on math autopilot.

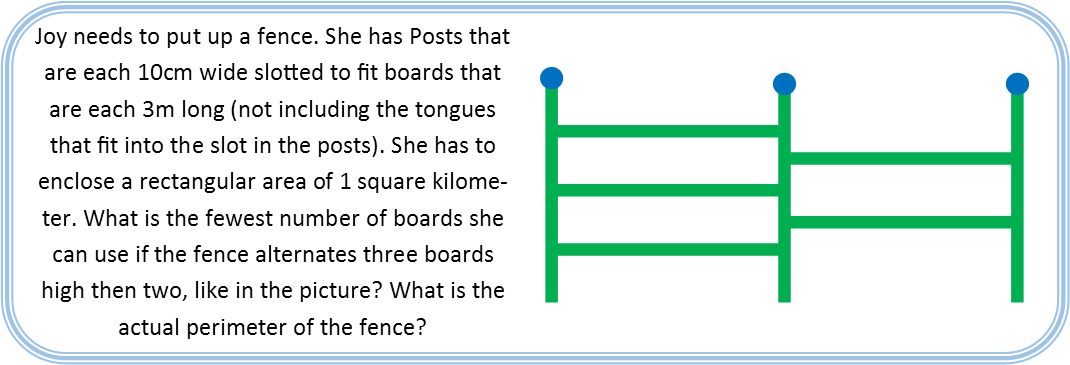
The very first thing I notice in the problem is my units aren’t consistent, so I’m going to convert everything to meters.

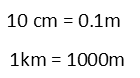
I also notice this is a perimeter problem, but around a given area without known dimensions of length and width. I’m being asked, essentially, what is the smallest perimeter that will enclose the given area? Since my boards are rigid, and not circular, I know that the minimum perimeter for a given rectangular area is a square, so I know all sides are equal. That means each side is about 1000 meters. I say about, because the fixed length of the posts and boards is going to make the fence actually a little larger than 1000 meters to a side.

Now to calculate how many boards to a side. I’m going to plant the first post, and then ignore it. Why? Well, we don’t need two posts on a corner. Look at the picture below. To achieve that, I have to take a post off of each side. In fact, the last side I even have to remove the last post (But that doesn’t affect how many boards to that side because nothing follows that post).

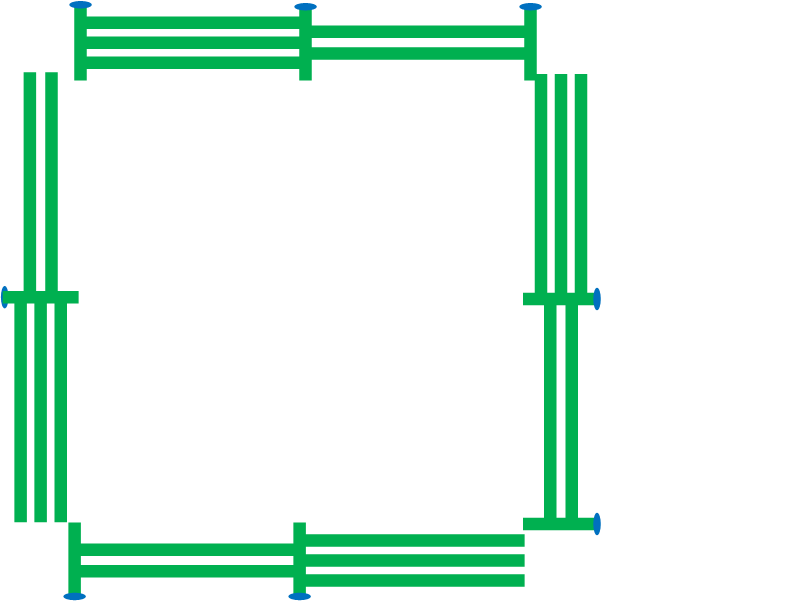
So if I treat each section as comprised of one 3-board length, and one 2-board, I seed that the length of each section is 2 posts plus 2 boards. So to determine how many sections to a side, I divide 1000 meters by the total length of 2 posts plus 2 boards.

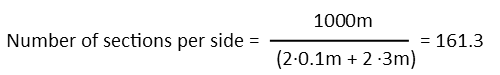
Which turns out to 161.3 sections. I can’t have a third of a section, but I CAN just put in one more set of board to finish the side (I have to or my fence will enclose LESS than 1 square kilometer, which we don’t want). Since the first section of the first side starts with a 3-board part, 161 sections end with 2. So the additional boards there is 3. I multiply the number of whole sections times 5 (5 boards per section), and add in the extra 3. For the second side, since I’m alternating, I have to start with a 2-board part. That means when I get to the end, my extra bit has 2 boards. So to find the boards on that side, I do the same that I did on the first side, only I add 2 instead of three. The third side is identical to the first side, and the 4th side identical to the second.

Now that I know how many boards each side has, I just sum them.

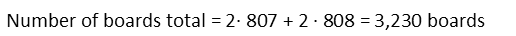
Now for the actual perimeter of the fence. Since I one extra length of boards, and an extra post, the length of any side is the length of 161 sections plus one post plus one board. A section length is the width of 2 posts plus the length of two boards. The perimeter of the fence is just 4 times the length of a side (since they’re all equal length).

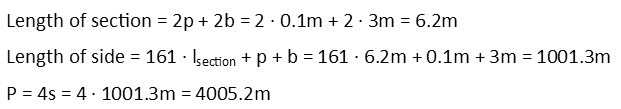
So we had to be careful when considering both how many boards the fence included, as well as how many sides. We had to realize we could express the fence in sections to make it easy, but that each section also ignored that first post, or we’d be doubling up posts. Then we also had to recognize that we can’t have a fraction of a board, and not fall into the trap of rounding up sections, but instead just adding one board length (since we COULD do that). Remember that math is a tool – make it work for you, not for it. That means using your critical thinking skills to avoid letting your math tell you something that is just wrong.