Math Made Easy: Problem of the Day 37

Today’s problem is straight out of the SAT. Let’s take a look at it.

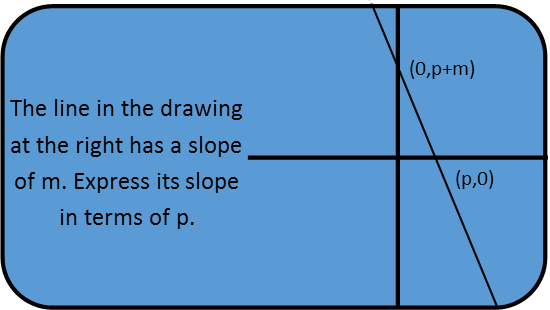
It really just requires a bit of juggling. First, we need to recognize that slope equals rise over run, and we can find the slope of a line from any two points on the line with the following equation:

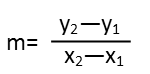
And since the slope of this line IS m, we can just plug the points into that equation. It doesn’t matter which one we call point 1 and which we call point 2, as long as we’re consistent, and the y coordinates go on top while the x coordinates go on bottom. Once we do that, we solve. I see that m is both sides of the equation, and to solve for the slope in terms of p, I need to get m on its lonesome on one side of the equation, with everything else on the other. Since it’s in a fraction with p, the first thing I’m going to do is break up that fraction. I see I have a constant in part of it since p/p is just one, and I write it as such.

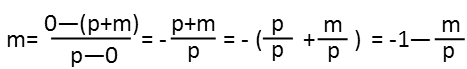
I then move the 1 to the m side of the equation by adding 1 to both sides. After that, I divide both sides by m so that my m’s and p’s are no longer all mixed up.

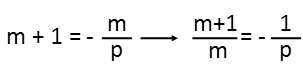
I at least have all my variables separated, but m’s not all alone yet. I still have work to do. Just as I broke up the original fraction, I’m going to break up my new fraction, and I again see I have 1 in the form of m/m, so I write it as such.

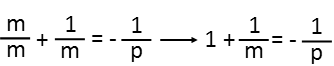
Then I move the 1 BACK over to the side of the equation with p by subtracting it from both sides of the equation. Well, look at that, m is on its lonesome. BUT, it’s on the bottom of a fraction. That’s no good, but it’s easily resolved by taking the reciprocal of both sides of the equation. Before I can do that, I need to combine the p-side into one fraction. I find a common denominator by multiplying 1 by p/p, and add them.

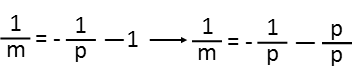
Note that I recognize I could factor that negative sign out of both fractions resulting in a negative fraction but 1 and p being added in the numerator rather than subtracted. Once I have both sides expressed as fractions, I just flip everything (the reciprocal). Lo and behold, after a little bit of creative juggling, we’re done. We have the slope, m, expressed in terms of the variable p.
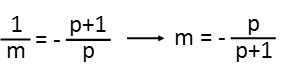