Math Made Easy: Problem of the Day 38

It’s time for some more physics. Today’s problem is more straight forward than usual.

We really only need to find one thing here – how do we relate the energy it takes to raise something’s temperature to that temperature increase? Well, we have a very simple formula for that, and it involves the mass of the object, its specific heat index (a numeric representation of the object’s ability to retain heat), and, guess what, the change in temperature. It looks like this:

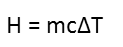
We know the mass of the atmosphere, as it’s been calculated and cross-checked by many scientists from different disciplines, and we know the specific heat capacity of air, as that’s been measured.

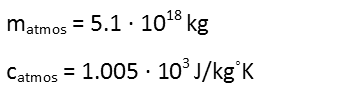
So we plug those into our equation to find out how much energy we need to raise that temperature. Note that degrees Celsius and degrees Kelvin are the same scale with shifted starting points, so a change of 0.1 degrees Celsius is the same as one of 0.1 degrees Kelvin.

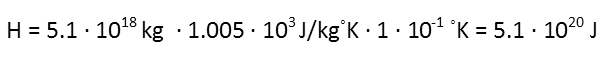
Now that we have that, we need to use the same equation to find the temperature increase of water. We can calculate the mass of the water from its volume, and since density is actually defined in the metric system so that water’s density is 1, we know that 2.5 million liters of water has a mass of 2.5 million kilograms. We also know the specific heat capacity of water, as it’s been measured.

We solve the equation for temperature, and then we plug in the energy we obtained from the first equation as well as the mass and specific heat capacity of water.

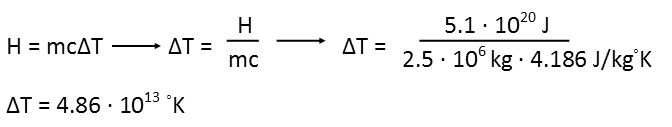
And we see that that would raise the temperature of the swimming pool to a frightening degree, literally vaporizing the water and anything in it. Even though air can’t hold as much heat as water, the atmosphere is vast, and the swimming pool tiny. But also recognize that this means that when we talk about increases in the average global temperature, ANY increase is significant, as the energy required to shift the temperature of that large a mass is enormous.