Math Made Easy: Problem of the Day 39
Sometimes in math, it is useful to compare quantities that are dissimilar. For example, when we need to scale a structure, we may need to compare its volume to the length of one if its sides. We they might have different dimensions, or a different source, but we learn something about the physical reality of the situation from comparing them. Thatís what todayís problem is about.
First, letís draw a new picture, with two full circles and an equilateral triangle, and mark the radii so we can better see whatís going on.
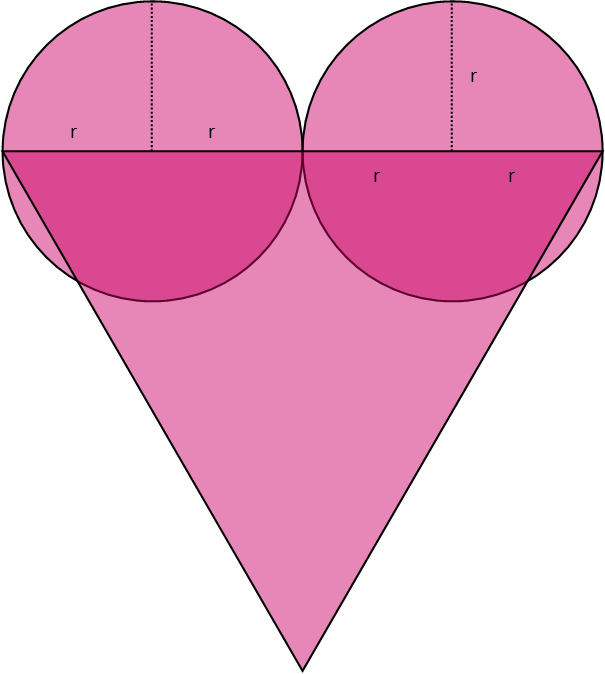
Now we can work on the equations. For the perimeter of the object, I see that the circumference of one circle is the same as the portion of the perimeter made up by the two semicircles. I further see that the triangle contributes two of its sides to the perimeter. Each of those sides is equal to 4 of the semicirclesí radii, as we can see in the drawing. Iíll write my equation for the perimeter recognizing all of this, and express it all in terms of the radius of the semicircles.
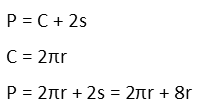
For the area of the shape, we can recognize that the area contributed by the semicircles is equal to the area of one circle. The area contributed by the triangle can be found with the general formula for a triangleís area, recognizing that a=b=4r, and that, for an equilateral triangle θ is π/3, and the sine of that is √3/2. So we simply sum the area of a circle and the area of the triangle in terms of r to find the area of the figure.
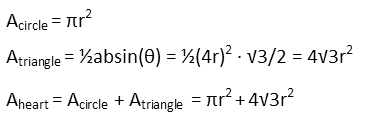
To find the point where the magnitude of the perimeter equals the magnitude of the area, we set the formula we found for the perimeter equal to the formula we found for the area, and solve.
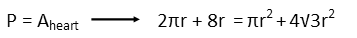
I recognize that every term has at least one r in it, so Iíll divide both sides of the equation by r to simplify. With an r left in both terms on the right-hand side, Iíll factor that out on the right.
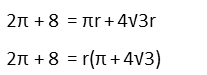
Now Iíll move the parenthetical constant on the right over to the left-hand side of the equation by dividing both sides by it.
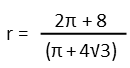
I can put this into a calculator or computer now to find the decimal value, but Iíd like to rationalize the fraction so I can have it for an exact value should I need it at a later date. To rationalize, since I see that radical in the bottom is involved in a binomial, I need to multiply top and bottom by that binomialís conjugate.

Itís an ugly fraction we end up with, but itís the form we want it in for possible later use. Evaluated, we see the radius needs to be about 1.418 for the magnitude of the perimeter to equal the magnitude of the area of this particular figure. And what does this value tell us? Well, when the radius is below that, the perimeter will have a larger magnitude than the area. When it is higher, the area will have the higher magnitude. Which could help when you're trying to figure out the quantities of building materials you need when scaling a structure.
The lesson of the day: donít get hung up on different dimensions when asked to compare items with differing dimensions. It is possible, and it can gives us some physical realities we might need (like how do we scale a ship with a given shape).
|



