Math Made Easy: Problem of the Day 4

Today’s problem is short and sweet. It tests your ability to group and deal with exponents. Here it is:

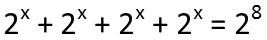
Now some people, as soon as they see a variable in the exponent, freeze up and stop thinking. Don’t fall into that trap. Just remember the math still works exactly the same, and look for ways to change the expression to your advantage. You *could* use logarithm rules to solve this equation, but you don’t need to do so. Frequently, when you’re handling exponential equations, their solutions are much easier and never need to involve logarithms. This is one of those cases.

First thing we should do, is regroup everything. I see that, on the left side, not only do I have a common base, but I have the exact same term 4 times. So instead of worrying about how do I add exponential terms, I’m going to change this into a multiplication problem. Since I have 4 of them, I simply rewrite it so. Further, I see that 4 is a power of two, and all my exponentials have a base 2, so I’m going to write that 4 as a power of 2, like so:

Now I’ll divide both sides by 2², eliminating it from the left side. On the right, we have the rule for dividing exponential terms with common bases, where we simply subtract the denominator’s exponent from the numerator to get our result: 8-2=6, so we end up with 2⁶. And now that we have one term on either side of the equation, both with the same base, and no coefficients, the base no longer matters. We can ignore it completely. Our solution is x=6.

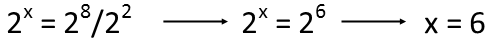
And, just to make sure we did our math right, we can always test it. 2⁶=64. 64+64+64+64=256. And 2⁸ is indeed 256. Beautiful!

So remember, when solving exponential equations, you don’t always need logarithms. It’s much easier if you can find a way to rewrite everything so that you can just ignore the bases.