Math Made Easy: Problem of the Day 40

The whole point of algebra is to take an expression which is in a form wherein the answer is not obvious, and via a series of operation where we don’t change the value of the expression, change it to a form where we can better see the answer. Today’s problem tests your ability to use your algebra to work with exponents.

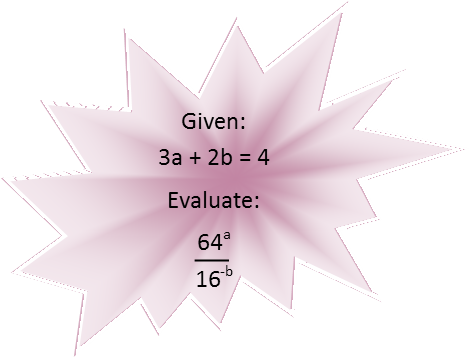
When working with exponentials, it’s frequently helpful to rewrite them in a different form. With this fraction, I see there is a negative exponent on the bottom. And since a negative exponent is really just telling me to move that term from the part of the fraction it’s in to the other, I’m going to let that migrate to the top, effectively turning this into a multiplication problem instead of a division problem. Next, I want to get a common base for my exponentials so that I can actually invoke the product rule for exponents with them. Remember that the product rule does not work unless the terms have a common base.

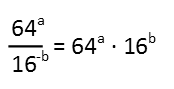
Looking for that common base, I recognize that 16 and 64 are both powers of 2 and 4. But which one do I want to use as the common base? The clue is in the linear equation we were given. If I can, I want to see a 3 in the exponent of the a term and a 2 in the exponent of the b term. 16 is 2⁴ and 64 is 2⁶. Now I could get a 2 and 3 out of those by factoring, but I don’t think I really want to use 2 for my base, so I’m going to look at 4. Well, 16 is 4² and 64 is 4³. Perfect! I’ll use a base of 4. Rewriting the expression with that, I have:

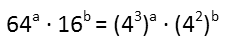
Now I can invoke the power rule to evalute the parentheticals (which tells us that, when we have an exponent raised to another exponent, we multiply them) and then the product rule, which tells us to add exponents when we're multiplying exponential terms with like bases. Doing so, we get the following:

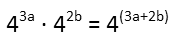
Oh, look! That looks like part of our linear equation! Beautiful! That’s exactly what we wanted. So now I can just substitute the value (4) of our linear equation for the 3a + b in our exponent, and finish evaluating.

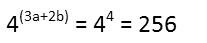
Our answer is 256.

Rewriting your expressions saves the day more often than not. And remember to look at your conditions and constraints to help give yourself an idea of what you want your expression to end up looking like, as that’ll guide you in your choices, especially when you have more than one way to rewrite it, as we did for today’s problem.