Math Made Easy: Problem of the Day 41
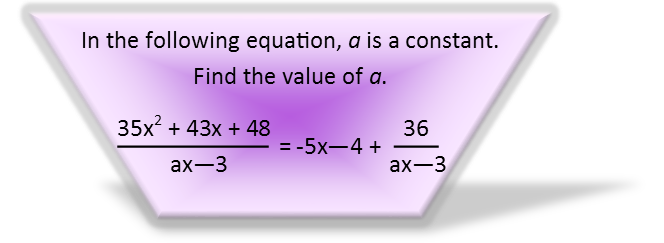
Problems like todayís require that you donít get too hung up in solving the equation. Since we donít yet know the constant a, we effectively have two variables until we find it. So what we first need to do, is get that equation into a form where we can more easily see just what a is.
I see that we have two fractions in the equation, both with the same denominator. So, to get rid of those fractions, Iím going to multiply both sides of the equation by that denominator.
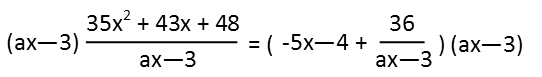
It cancels out of both the fractions, and leaves me with a nice quadratic on the left side. On the right side, I have what looks like two factors of a quadratic plus a constant.
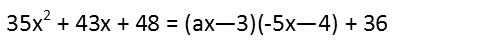
Using FOIL (First Outside Inside Last) to multiply those two parenthetical factors, I expand them.
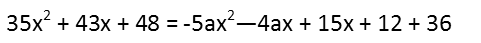
The two sides donít look too similar now except for the fact that the constants add up to the same value.
Thatís good. But what I do see, is that I can set up two equations for a. I recognize that, since there is only one squared term, that a must be whatever I need to multiply that coefficient of negative 5 by to get 35. It must also satisfy whatever I need to multiply -4 by to get 43 after adding 15. Thereís only one possible number that will satisfy both requirements, and thatís -7.
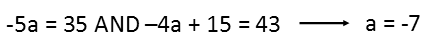
Todayís problem was actually very simple. It required less explanation than many of the problems Iíve done. The key was not trying to actually solve the equation, but just trying to put it in a form where I can find equations for the constant I was seeking. Itís another reminder to avoid math autopilot.
|



