Math Made Easy: Problem of the Day 42

Most people learn about the different ways you can find the middle of a group of numbers in high school. But you usually only learn three of them – the mean, median, and mode. Often, people either don’t learn, or forget, that there are two different kinds of mean – the arithmetic, and the geometric, and they have different meanings. The arithmetic mean is more commonly useful in every day financial situations, which is why you learn it in high school. The geometric mean is useful in physical situations (as the term geometric implies), as well as more complicated mathematics, as economics can get. This problem really is about recognizing the different ways to find the middle, and what exactly they each mean.

So first, we have a geometric mean. That is defined as the root of the products of the numbers involved. Since we have two numbers, then it’s a square root (if it were three, we’d take the cube root, 4, the fourth root, and so on). So we can write the equation for x in terms of m (note I used fractional exponential notation to express the square root rather than that ugly radical operator):

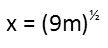
For y, we have an arithmetic mean. That simply means add up all the numbers, and divide by the count of the numbers (so divide by 2 if you have 2 numbers, 3 if you have 3, 4 if you have 4 numbers, and so on). Given the values for y we were given, we can write the equation for it:

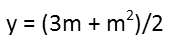
And, for z, we recognize that the median is just the middle-most number of a set of numbers. To find it, you write them out in numeric order, and start crossing out the outside-most numbers in pairs until you only have one number left (if you have an even amount of numbers, you’ll have two left at the end, in which case you just take their arithmetic mean). Here, we have an odd count of numbers, so the middlemost one is the median – that’ll be 4m, no matter what m is.

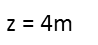
So now we recognize that the arithmetic mean of x, y, and z, is simply their sum divided by three, so we right an equation relating just that to their respective values in terms of m.

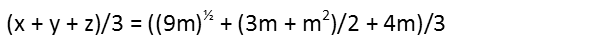
And now we simplify the expression on the right-hand side of that equation. I first recognize that I can take the square root of 9, so I pull that out of the square root, and at the same time, I distribute the ½ to the terms by which it’s being multiplied.

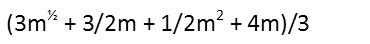
I then combine like terms, adding 3/2m to 4m.

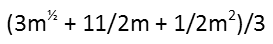
Finally, I distribute the ⅓. And we have our expression for the arithmetic mean of x, y, and z in terms of m. You can also reorder the expression in order of descending exponents if you like.

I initially wanted to make this a fully solveable problem, and had set m=4. That would give an arithmetic mean of x, y, and z of 12. x would have come out to 6, y to 14, and z to 16. But, after a lot of math so I could show you how to do it, I realized that you’d need the quartic formula to solve it. That formula is far more complex than the quadratic formula – enough so that’s it’s virtually impossible to make an image of it that fits nicely and legibly on one page. So it really was beyond the scope of these articles. BUT, for an added challenge, see if you can prove that m = 4 if the arithmetic mean of x, y, and z is 12. The key to that is to start with the expression we found for the arithmetic mean of x, y, and z in terms of m.