Math Made Easy: Problem of the Day 43

We’re going exponential again today. I like writing about exponents because a lot of the students who come to me struggle with them. The rules for them are simple, yet so many people seem to get mental blocks when they see them, it’s good to go over them and always remember what they are.

This problem is about two things: applying the power rule of exponents, and factoring. Let’s look at each equation in order.

For the xy equation, let’s start by distributing that exponent on the outside of the parentheticals, and multiply it by each exponent. That’s what the power rule tells us to do. A lot of texts like to break up the power rule into two rules, but it’s really just one – when you raise an exponent to another exponent, multiply the exponents. The second part of the power rule, where you distribute the exponent, is really just the distributive property of multiplication, so I think that trying to force students to memorize yet another rule actually causes more confusion than is necessary. So, when we apply the power rule, we get:

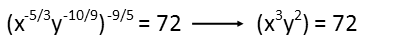
The next thing we need to do, is factor 72. I usually recommend the pair method, but for solving an exponential equation like this, where we have two variable to a power equaling a constant, the tree method will actually be superior for this problem.

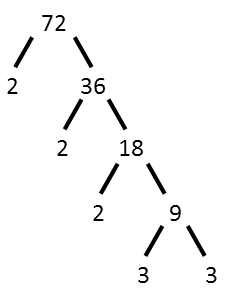
What we’re looking for, is factors that show up multiple times. For 72, we have 2 showing up 3 times, and 3 showing up twice. That tells us that 72 is made up of 2³ and 3². It’s convenient that those two exponents exactly match our x and y exponents, so we rewrite the equation with those factors, and then recognize that x = 2 and y = 3.

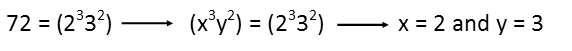
Now we do the same thing for the zq equation. First, distributing the outside exponent inside the parenthetical and multiply the fractions.

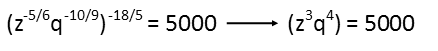
Now using the tree method to factor 5000.

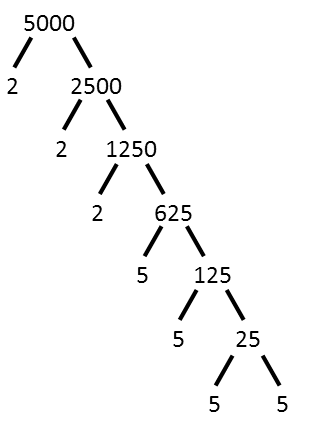
We see we have 3 twos and 4 fives, so 5000 is made up of 2³ and 5⁴. We rewrite the equation reflecting such, and recognize that z is 2 and q is 5.

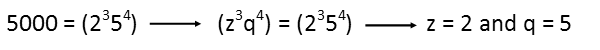
Finally, we plug x, y, and z into the final expression so we can evaluate it. Conveniently, x and y are both 2. And since a negative exponent just means put that number under a fraction, x will end up in the numerator (as will y), and z in the denominator, so x and z cancel, leaving us with just y². So we find our final answer is 9.

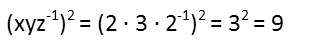
A pitfall one could find oneself stumbling into on a problem like this, is trying to evaluate whether the system of equations is solvable before working on them. Frequently that’s wise to do, because we don’t want to waste our time solving a system of equations that has no solution. To do so, we normally look at how many variables we have, and remind ourselves that, for every variable in a system of equations, we need at least one equation. So, normally, for this system, since we had 4 variables, we should need 4 equations. But by clever use of factoring, and recognizing those similar exponents, we found we actually *could* solve this system of equations.