Math Made Easy: Problem of the Day 44

We haven’t played around with series enough, so let’s do a new one today.

There are three basic types of series we can play with: arithmetic, geometric, and power series. In an arithmetic series, we simply have an additive to each term to find the next successive term. For geometric series, we multiply each term by a coefficient to find the next. And in a power series, we raise each term to a given power.

Before I resolve what kind of series it is, I’m going to take care of that alternating sign. In a previous article, we recognized that is was a trigonometric function, specifically the cosine, that was producing that fluctuation. For this series, we can use a simpler way to produce it, which is just raising (-1) to n power, where n is the current term in the series (First, second, third, etc). Now, ignoring that sign, since we can now that we’ve determine what’s producing it, we see that the gap between each succeeding term is growing, so this can’t be an arithmetic series. If it were a geometric series, we could find a common ratio, and we do that by dividing each term by the preceding term. The ration from 1 to 2 is 2. But from 2 to 9 is 4.5. So we do not have a common ratio, which means this isn’t a simple geometric series. But I see easily that each term after the second appears to be a power: 9 is 3², 64 is 4³, and 625 is 5⁴. Oh, that’s quite the nice pattern there, and can be expressed by n^n-1. I think we’ve found the expression generating our series, and it looks like this:

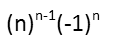
So to find the 11th term, we just plug 11 into all the n’s, and we get: -25,937,424,601. It’s negative since any odd power of -1 is going to be negative, and any even power is going to be positive. For an added challenge, calculate the sum of the first 20 terms. The first 50. The first 100. For this, you may need your calculus.