Math Made Easy: Problem of the Day 45

One of the reasons to practice your mathematics is to develop number familiarity. That is the sense you can gain where you have an almost intuitive feel for how numbers interact with each other. You can use that familiarity to help you solve some problems more easily, and to make seemingly impossible problems possible. Today’s problem is all about testing your familiarity with numbers.

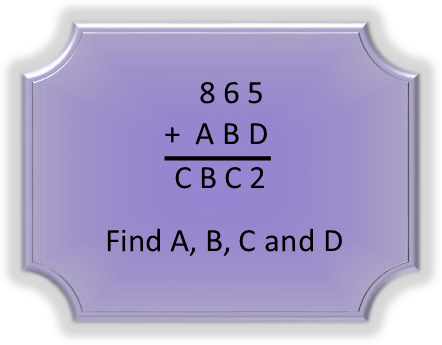
How do we solve this equation? At first glance, it looks like we have 4 variables. But we really don’t – they’re all constants. This is just a puzzle, and with our familiarity of how numbers work, we can solve it, if we approach it methodically, one letter (or number) at a time.

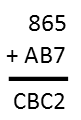
Let’s start with D. There is only one number that one can add to 5 that will result in a 2 as the last digit. That’s 7 (5 + 7 = 12). So we know D must be seven. We replace it with it and look at the next number.

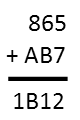
We can see a pattern with the Cs – they repeat. And our clue is in the first one. We’re only adding two numbers, and even if I carry a one over from whatever is being added to 6, there is no way we can add anything to 8+1 that will give us something in the 20s. So C MUST be a 1. So let’s replace the Cs with ones.

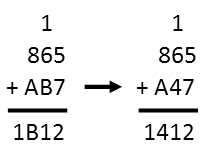
We can find B now. We carry that one over from 5 + 7, and write it on top of that column 6 + B = 1, so that we can more readily see what we have, which is really 1+ 6 + B = 1. The only thing we can add to 7 and get a one in the second digit is 4. So B must equal 4. We can now replace both Bs.

Finally, we do the same thing for the 8 + A = 4 column. This gives us 1 + 8 + A = 14, and the only number we can add to 9 to get 14 is 5. So we know A = 5. And we have all our letters, and we’ve solve the equation.

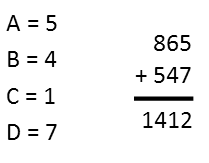
Number familiarity is an extremely useful skill, and the only way to develop it is to do math – play around with numbers, and you’ll build it soon enough.