Math Made Easy: Problem of the Day 46

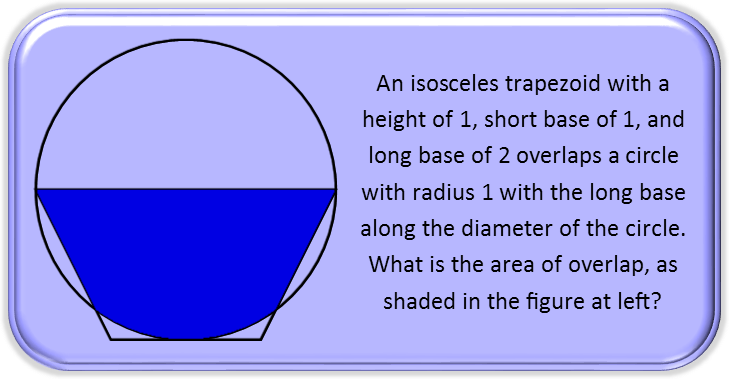
Today’s geometry problem may at first glance appear more difficult than it really is. To solve problems like this, we always need to look for ways to break the situation down into shapes and pieces that we know how to do. For this one, we can see that the area of overlap is essentially just the area of half the circle minus the area of those two little slivers, or segments, formed between the trapezoid and the circumference of the circle. But how do we calculate the area of those segments?

We know a basic formula for the calculate of the area of a circle segment, and it requires we know the measure of the subtending angle – that’s the angle formed when we connect the two points where the line making the segment meets the circumference of the circle are connected to the center of the circle. I’ve marked that in the figure below. To get that angle, we can solve the triangle formed. But to solve the triangle, we need at least two sides and one angle. We have two sides, since two of them are radii, but we don’t have an angle.

Or do we? As you can see in the figure above, I’ve extended the legs of the trapezoid to form a triangle. It turns out, that with isosceles trapezoids, we can set up a ratio of the distance from the top of the trapezoid to the vertex of the triangle over the height of the trapezoid. This ratio is directly proportional to the length of the top of the trapezoid to the length of half the base of the trapezoid. Here they’re 1:1. So the height of the triangle formed is 1 +1 = 2. This is helpful, because, as the figure shows, we can divide that bigger triangle into two smaller right triangles. One of those has one of the angles of the triangle we need to solve. We can get that angle by solving the right triangle, and taking the inverse sine of the angle.

So let’s find the hypotenuse of the right triangle using the Pythagorean Theorem first.

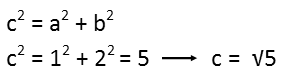
So now that we’ve done that, we know the sine of γ:

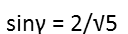
To find α, which is the angle we need, we can remind ourselves of the law of sines, where each angle is related to the side opposite it.

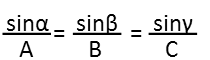
We don’t know the side opposite angle α, but we don’t actually need it. If we calculate angle β and subtract it and angle γ from π, we will have the measure of angle α in radians. So let’s first calculate the measure of angle β. Note I’m going to leave it in terms of angle &gamma and the sides. It’ll actually make my calculations easier later. Another point of interest, is that since B=C=1, angle β = angle γ.

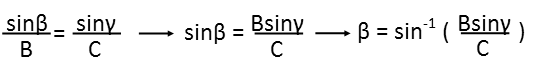
And now we calculate angle α. It’s actually quite convenient those two sides are both 1 unit long.

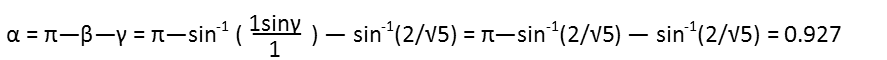
Now that we have angle &alpha, we can calculate the area of the segments. The formula for the area of a segment of a circle is found in the form with which I start the following equation. The area of those segments is really small, so I’m going to leave it in the expression form rather than the rounded decimal form for accuracy’s sake.

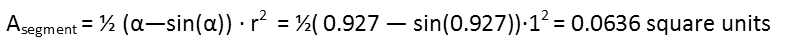
With that, we can now calculate the area of overlap by subtracting two segments from half the area of the circle:

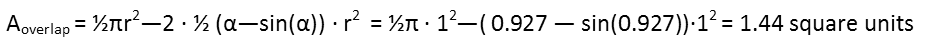
The major point of today’s problem is to not let a seemingly daunting task intimidate you. Break it down into parts, find what you can, and find creative ways to fit shapes you do know how to solve into the ones you’re being asked to calculate.