Math Made Easy: Problem of the Day 47

Today’s problem is another reminder that, while there is often more than one approach to a mathematical problem, not all of them are equally expedient. It is up to you to master multiple math techniques, and decide which works best for you in different situations. In that regard, I’ll attack this problem with two different techniques, starting with the one I personally think is slower first.

The slow method, in my opinion, is to solve the system of equations as a system of equations using the substitution method. To do that, I start by taking the first equation, and solving for b in terms of a.

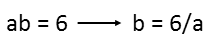
I then plug that in for b in the second (bc) equation.

That result I plug in the third (cd) equation.

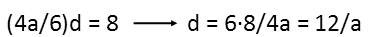
Whose result I substitute into the fourth (de) equation.

Finally, I replace e in the fifth (ae) equation with that result. I now have an equation entirely in terms of a, so I solve for a.

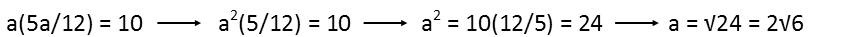
Once I have my value for a, I can just plug that into the first equation, find b, plug that into the second equation, and so on until I’ve found the correct value for all five variables.

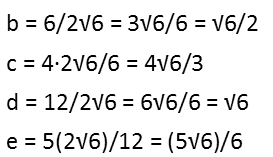
Now that I have the correct value for all five variables, I simply multiply them to find my final answer.

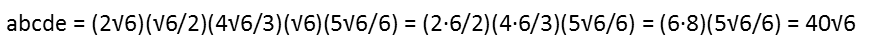
Not counting solving for each equation, that method had seven steps. The method I recommend, however, has far fewer. In fact, including solving the equation we set up, it only has 4 steps. In this method, we recognize that if we multiply the left hand side of all five equations, we’ll get a result of all the variables squared. So if we just multiply all the left and right hand sides of the equations, and take the square root of the result, we’ll get our answer more quickly.

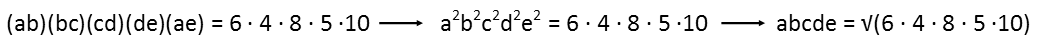
Note that as I do this, I’m computing the right-hand side of the multiplication until the end. In fact, I actually break down the numbers in the second-to-last step so I can more readily see perfect squares and pairs that I can pull out of the root.

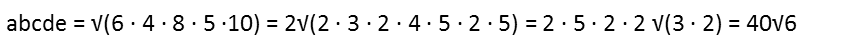
We get the same result with both methods, but the second, to me, is much easier. We don’t have to solve multiple equations for it, and we don’t have to juggle that √6 all over the place. But if substitution works better for you, by all means, use it. The mathematical toolbox is there to work for you, not the other way around.