Math Made Easy: Problem of the Day 48

We haven’t done much with finding the domain of a function yet, so I decide to do one for today. The domain of a function is all the possible values of x that will produce a real result. If it produces a complex number, it is not considered to be in the domain, and if it produces a null result – in other words, a result where the function can’t exist because you’re asking the math to produce something physically impossible – then it also is not in the domain.

Finding the domain of a compound function must be done in steps. First, you must assess the domains of the individual functions – if any value of x invalidates any of the component functions, it does not exist in the domain of the composite function. And with any function or expression, you must address its domain both before AND after simplifying the expression (for example x²/x, even though it simplifies to just x, exists for all values of x EXCEPT zero, since that would require us to divide by zero if we inserted zero for x before simplifying the expression).

So let’s start with f(x). First we see that sin(x) is in the denominator. Therefor any value of x, when inserted to the sine function, that produces zero, is invalid. The sine function equals zero when x equals zero or any multiple of π. So these values are now restricted from our domain. The composite function cannot exist there.

We also have the tangent in f(x). The tangent is sin/cos. This means the tangent does not exist anywhere that the cos(x) = 0. This happens at any multiple of π/2. So these values are also excluded from the domain. Note that the notation I use here reads as follows: “x is in all real numbers such that x does not equal any integer times π divided by two.”

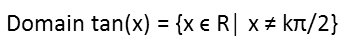
So putting those restrictions together, we get the domain of f(x):

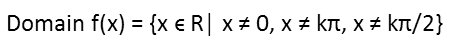
Time to look at g(x). We have 1 – sine(x) on the bottom of the fraction. So, again, anything that produces zero in the bottom is no good, and that would be any place sine(x) = 1. That’s going to be any multiple of &pi/2. We’ve already excluded those values from our domain, but I’m going to write it down anyway.

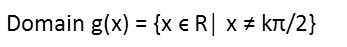
We’ve already restricted the domain of this composite function by quite a bit, but there’s more to go. Let’s look at h(x) now. It’s a square root, and any square root that has a negative value inside will produce an imaginary number, so anything that does that will be excluded from our domain. Since it’s negative x inside that square root, all positive values of x are excluded. So x must be less than zero.

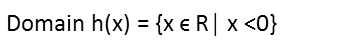
So our current domain of our composite function φ is:

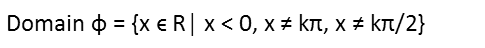
Note I did not include the qualification that x cannot equal zero since that is satisfied by the requirement that x must be less than zero.

Now, let’s put all our functions together to see what they look like as a composite function, before simplifying. We need to do this to see if the domain restricts further. We do this simply by replacing each function with its expression. If any function is inside another function, we put its expression wherever we see x inside that other function. Our composite function looks like this before simplifying:

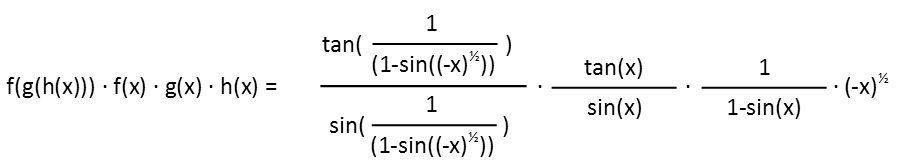
I see that we have 1 – sin((-x)²)) in two denominators. So this means that any square of negative x, that, after taking its square root, produces a 1 when placed inside the sine function, is now excluded from our domain since that would put a zero in a denominator. So x cannot be any square integer multiple of π²/4, since the square root of that will always be a multiple of π/2, where the sine will equal 1. Let’s add that restriction to our domain now.

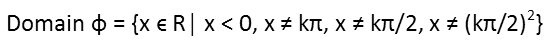
We now need to consider when sine(junk) = 0, since we now have sine(junk) in one of our denominators as well. This, again, is going to be any time when that junk is any multiple of π. So we need to solve the inside of that sine to find when it equals a multiple of π. To do so, I’ll set it equal to kπ and solve. Once I have x in terms of the inverse cosine, I can recognize that the only thing inside that inverse cosine that’ll give a zero for x is any multiple of π. So once I get that, I take the inside of the inverse sine, set it equal to kπ and solve that. If it has no real solutions, then there are no exclusions to our domain from this.

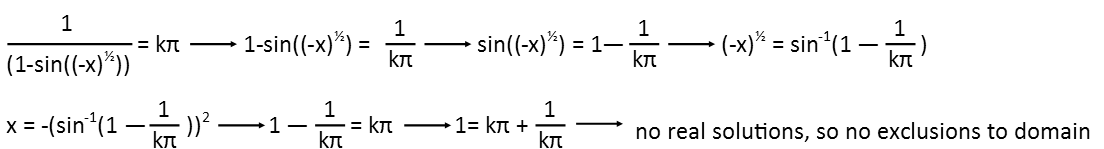
Now it’s time to actually start trying to simplify our composite function. I’m going to start with those tangents and sines, and just call the junk inside them u for now for simplicity’s sake until I resolve the sines and tangents. I recognize that the tangent is just sin/cos, so putting a sine under that cancels the sine on the top of the tangent.

After cancelling those sines, and putting everything back together and combining everything to one fraction, we get the following for our composite function.

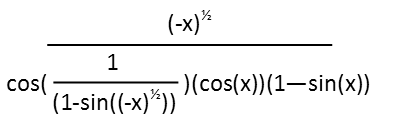
It’s still ugly, but it’s a lot simpler than we started. We could evaluate that cos/(1-sin) in terms of tangents and secants if we wanted, but it doesn’t really make the domain any more obvious. One thing we can see, is we’ve already evaluated all the situations that’ll produce zero in the denominator. So our domain doesn’t change at all now that we have this in simpler form. So our domain for this function is all real number where x is less than zero, does not equal a multiple of π or π/2, and does not equal a square of a multiple of π/2. So this function has a lot of places that it just simply does not exist.

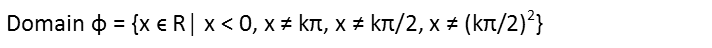
It’s necessary and useful to evaluate the domain of a function because it tells us something about the physical reality of what’s going on. It also lets us know where we don’t need to waste our effort banging our head over the problem – if a function doesn’t exist in a given domain, we don’t need to worry about that particular area.