Math Made Easy: Problem of the Day 49

For a problem like today’s, the first key is to just not let yourself get lost in the wording. Break it down piece by piece, and try to make sense of everything. This one is all about fractions. One could use an assumption method to try to solve it, but, really, that actually causes more work than is needed. If we think in fractions, of how they work, and stay in fractions for the entire problem, it’s actually quite easy. We first recognize that, since there are five shareholders who start out with an even number of shares, everybody starts off with 1/5 of the company’s stock.

We’re going to look at Mr Glass’s acquisitions first. Everything he buys is added to his original 1/5, so we’ll start his computation with that 1/5, and just add everything to that. Since he bought a portion of three other people’s stock, we multiply their original portion times whatever fraction of it he acquired, and add that into our equation. When multiplying fractions, remember top multiplies top and bottom multiplies bottom. If you can simplify before you multiply, absolutely do so (cancel like numbers from top and bottom in pairs). Here we have a bunch of ones on top, so the multiplication’s pretty easy.

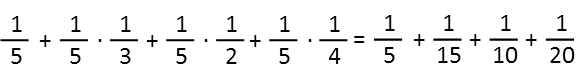
Once we’ve done the multiplying, we just need to add. Remember we need a common denominator to add fractions, and to get that, we just multiply each fraction by the version of one that is made up of a fraction whose top and bottom will multiply by the denominator of the original fraction to give us the bottom we want. Here we want a common bottom of 60, since that’s the first number that 5, 15, 10, and 20 all go into. Also remember that, when finding a common denominator, this is the ONLY time we do NOT want to simplify before we multiply – if we do, we defeat the purpose. Also note that after I found the common denominator, I didn’t bother writing separate fractions, I just wrote the products of the top plus each other all above that 60.

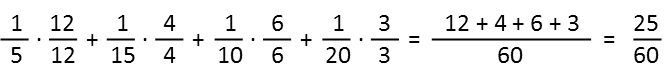
Once we have our sum, we can simplify. We see that Mr Glass has a little under half the company after his acquisitions.

Now to look at Ms Steel. Since she bought from the remainder, we have an additional step. BUT, we can still do the multiplying all in one step if we’re clever. We do this by first recognizing that the three sellers have left of their stock is just equal to 1 represented as a fraction with the same denominator as the portion they sold (so for ¼, we represent 1 as 4/4) minus that portion the sold. So, since Mr Ball sold 1/3rd of his stock, he has 2/3rds of it left. Ms Davenport has half left, and Ms Feynman has ¾ left. The additional step here, is we recognize that 75% represented as a fraction is 3/4ths (just remember there are 4 quarters in a dollar, and 3 quarters are 75 cents), so we multiply the products by 3/4ths. But we include it all in one step by recognizing that the product of a product is just the three things times each other in a chain, like I’ve written below. Also note that, though I usually show my cancellations with red line cross-outs, I actually did cancel those threes in Mr Ball’s product before I multiplied.

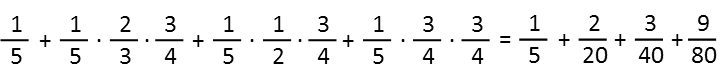
And now we find a common denominator, which is 80, and add.

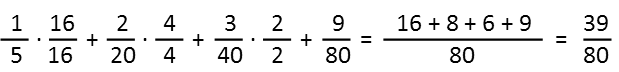
Another way we could have calculated Ms Steel’s shares, is to take advantage of that fact that, if we know that Mr Glass now has 5/12ths of the company, and Ms Steel 1/5th, we can find the total remaining shares before Ms Steel makes her purchase by subtracting her shares from what Mr Glass doesn’t own –which would be 7/12ths of the company. I did that below, making sure to give the fractions a common denominator so I could subtract.

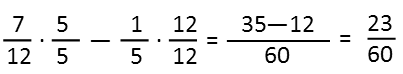
Then we multiply that by 3/4ths, since she bought three fourths of those remaining shares. To that product, we add her original 1/5th. And it turns out we get the same exact answer.

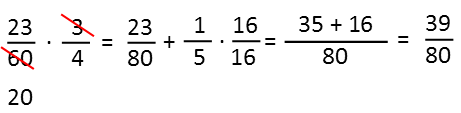
We can’t simplify that, but we don’t need to in order to compare the two fractions. Neither of them has a true majority (more than half) of the shares, but Ms Steel has the most, so would be considered the majority shareholder of this company. We realize that since 39/80 is clearly much closer to ½ than 5/12 is. So remember that, when you have a chance to work and stay in fractions, do so! It’ll almost always make your life easier.