Math Made Easy: Problem of the Day 5

Today, let’s tackle a problem that really demonstrates how math is useful in the real world. Kids, especially teenagers, frequently ask why they need to learn all that math, and how is it ever going to be of use to them in real life. Well, this situation is like one someone just might run into in handicrafts, an area where many people don’t think they need any mathematical skills.

Here’s the situation.

A painter is painting a logo for a company. The painter needs to know how much paint he needs. The company wants the blue circle to have a diameter of 2 meters. The painter has already figured out that every can of paint he uses can cover exactly one square meter. So how many cans of blue paint does he need? And purple paint? The logo is comprised of three shapes – a solid blue circle inscribed inside a black square outline inscribed inside a solid purple circle. The image below is what it looks like. See if you can complete the problem on your own before looking for the answers down below.

The first thing we need to do is figure out the dimensions of all our shapes. If the blue circle has a diameter of 2 meters, its radius is half that, or 1 meter. The sides of the square must be exactly the same length as the diameter of the blue circle inscribed in it (if you don’t believe me, shift it until the side is going straight through the center of the circle and you’ll see it’s true), so it’s got sides of 2 meters each.

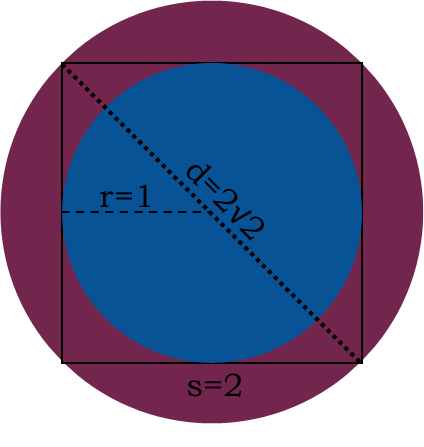
From that, we can figure out the diameter of the purple circle. It turns out its diameter is the same as the diagonal of the square. And that we can determine using the good ol’ Pythagorean Theorem.

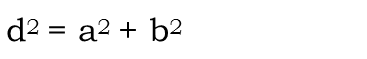
What’s even better, is the sides of the square are all the same, so in the Pythagorean theorem for the square, a=b=s. So from just that one piece of information, the radius of the blue circle, we’re able to find the radius of the purple circle, which is half its diameter, or half the diagonal of the square, and that comes to √2.

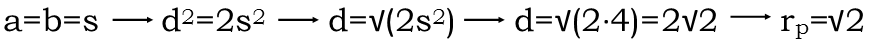
So now that we know the radii of both circles, we can figure out their areas. Reminding ourselves of the formula for the area of a circle, we have the following. Note that I used the subscript b for the blue circle and the subscript p for the purple circle.

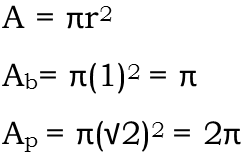
But looking at the logo, we see that the painter doesn’t need enough purple paint to paint the entire purple circle. He only needs enough to paint the area of it outside the blue circle. Which is the same thing is if we took the whole purple circle and took out the part of it the blue circle covers. In other words, we subtract the area of the blue circle from that of the purple circle.

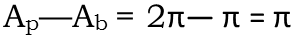
Now we know how much area he needs to paint of both the blue and purple circles. He needs to paint exactly π square meters with blue paint and the same π square meters with purple paint. But I don’t think any store will sell him π cans of paint, since no one wants a partial can of paint. He needs to round up, which means he needs to buy exactly 4 cans of blue paint, and 4 of purple paint. He’ll just have a little bit of each left over, perhaps for touch-ups later, or for another project.

And here we see how we used math, particularly geometry and the good ol’ Pythagorean Theorem, to accomplish a real world task. If the painter hadn’t calculated beforehand how much paint he needed, he might have bought too much, or too little. It pays to know your math.