Math Made Easy: Problem of the Day 50

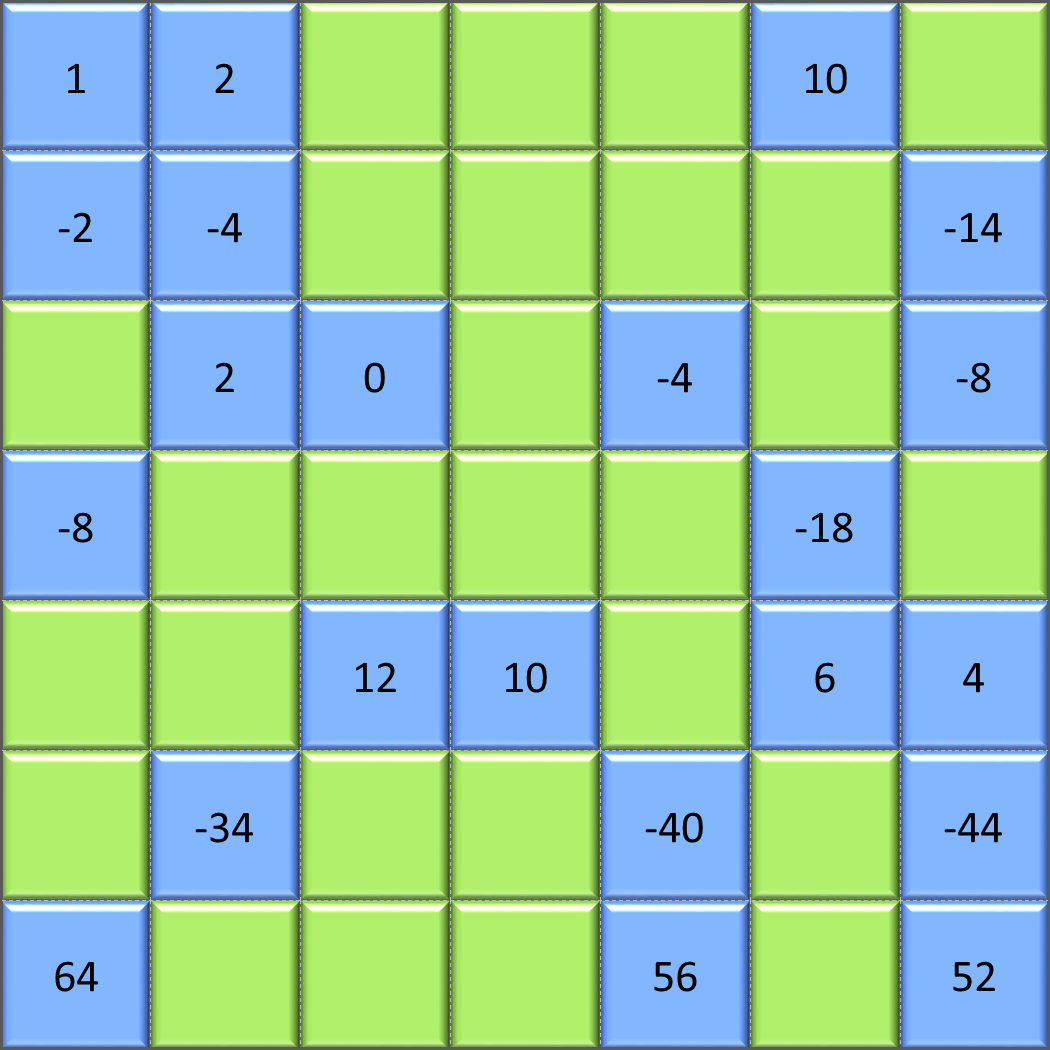
It’s the 50th Problem of the Day article! Woohoo! So to celebrate 50, I have another number puzzle for you.

The key to these is to always try to figure out a set of rules to determine what numbers go in each cell. So we examine rows and columns to find patterns. The top row isn’t very informative – only three numbers in it, and the relationship may not be obvious. So let’s look at the first column to start instead, since it’s already over half filled out. Ignoring signs, I see that 2, 8, and 64 are all powers of two. And we can express 1 as a power of 2, as well. In fact, we should recognize the column is a power series of -2^n-1. That negative sign inside the root will beautifully produce the -2 since that’s (-2)¹ as well as the -8 since that’s also an odd power. 64 is an even power, so it’ll be positive,

Okay, that first column was easy.

But what is the rule for the top row? Since the rule isn’t obvious from just look at the top row alone, let’s look at cells in the middle, that are the intersection of a row and column where we have the value in the top row’s cell that’s in that column as well as the first column’s cell that is in that row. So, I see that the 2nd cell in the first row is 2. It’s column intersections with the second row, who’s first cell is -2. There are two ways I can get -4 when I have -2 and 2 as my starting numbers. I can multiply them: -2x2 = -4. OR I can subtract 2 from -2: -2 – 2 = -4. Let’s see if we can find another intersecting cell. 10 and -8 intersect at -18. A-ha! There’s our tipper! If we multiply -8x10, we get -80. But if we subtract 10 from -8, we get -18. So the second equation seems to be the rule for the intersecting cells. We don’t have another intersection to test, BUT, we can predict what numbers go in the first row from the rule we’re proposing. To get 52 from 64, I need to subtract 12. And to get 56 from 64, I need to subtract 8. This would give us in the top row: 8,10,12. If I project all the way backwards, and include the two values we know at the beginning of the row, we’ get: 1,2,4,6,8,10,12. It fits the row, and we see a nice pattern if we ignore the 1.

After filling in that top row, and knowing a rule to determine the column, it looks like our rule for the intersection cells is subtracting the cell at the top of the column from the cell at the beginning of the row. If we declare x=2, we can make a table with the rules for the cells, and it looks like this:

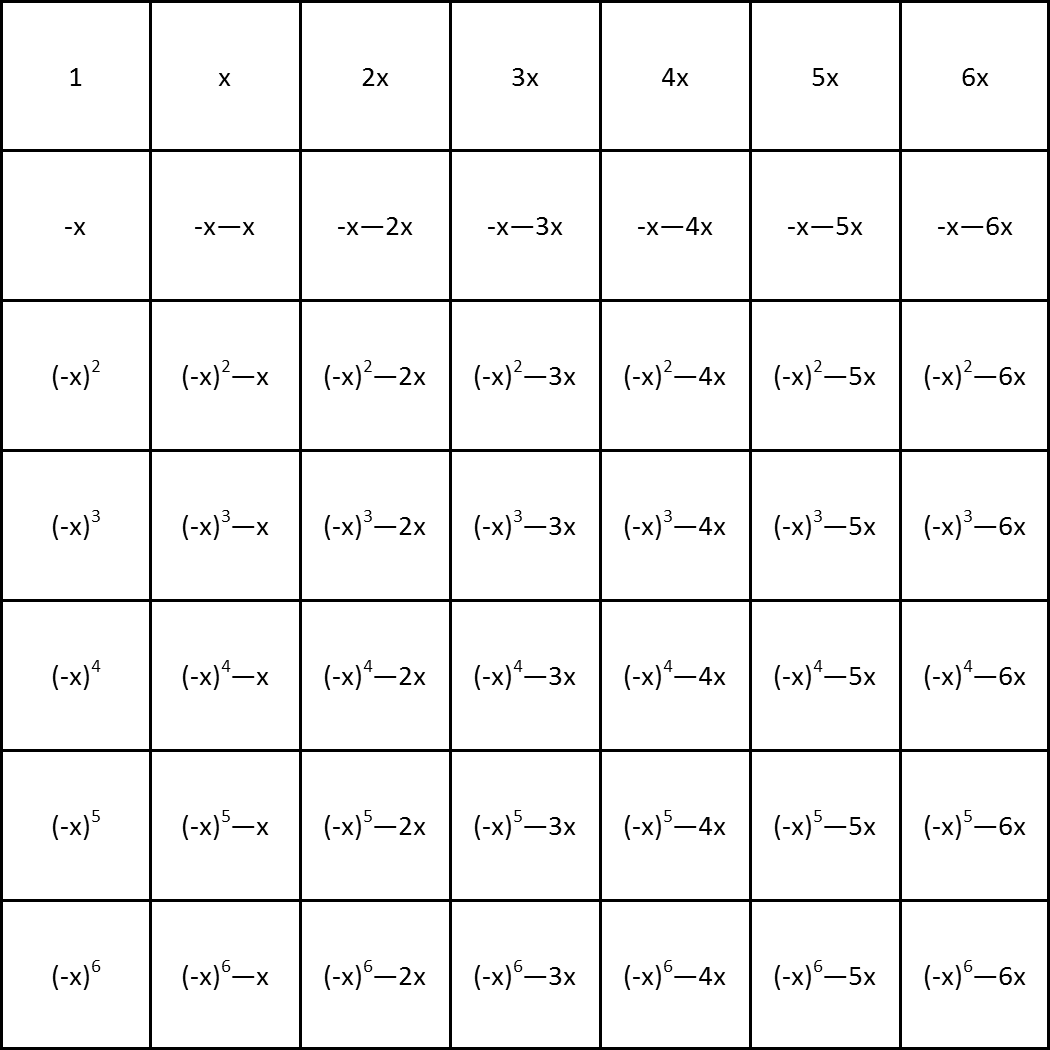
Now applying those rules, we complete the entire puzzle:

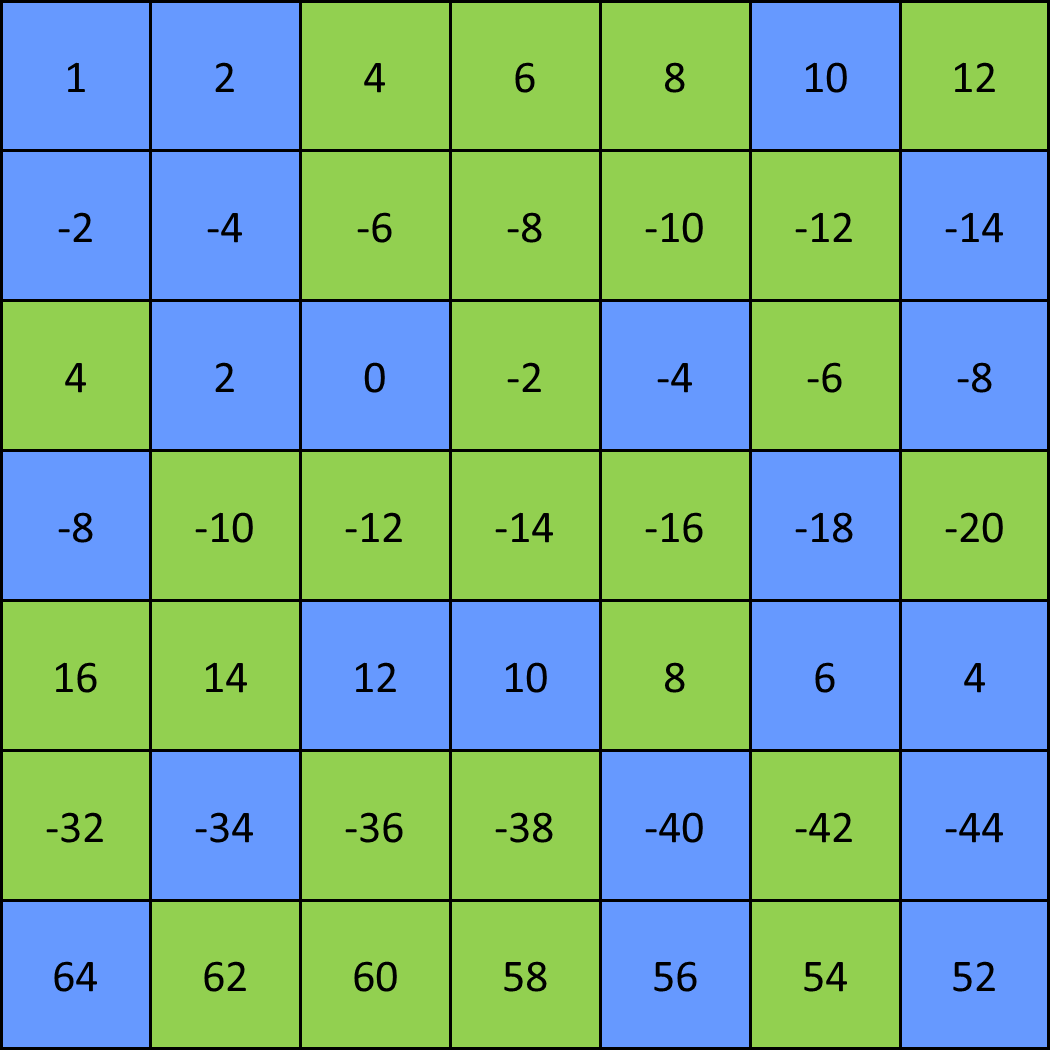
By the way, the 1 in the first cell, that was just there to confuse you. Note in the table I made for the rules, I just had a 1 there, since it doesn’t play into the rule for the first row. It was just happenstance that it can be expressed as a power of 2 (it can be expressed as a zero power of anything, so that’s going to happen when the rule is a simple power rule). I hope you enjoyed the puzzle!