Math Made Easy: Problem of the Day 51

For problems like todays, it’s best to first redraw the situation in a better scale. Label everything you can, like I’ve done so below.

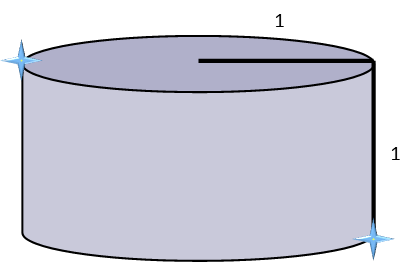
Now, it’s key to remember never to trust your eyes completely when dealing with geometry – they can deceive you. So let’s consider three different routes, and map all of them. We recognize we have to stay on the surface of the figure.

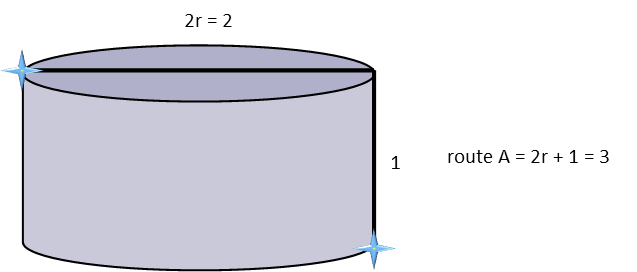
The first route we consider will be the simplest. We simply take the shortest route directly across the top disc of the cylinder from Toptown to the point directly above Downtown, which is the diameter (or twice the radius), then go straight down the height of the cylinder. This gives us a pretty simple distance where we just add the diameter to the height of the circle. This route is 3 units long.

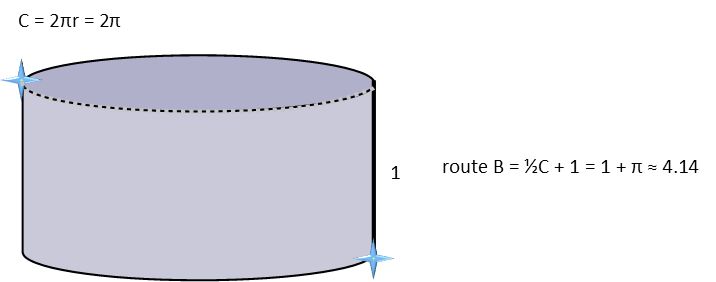
The second route we consider is one where we follow the circumference of the cylinder to that same point on the top disc directly above downtown. Since the two towns are diagonally opposite, this route takes half the circumference plus the height, which is about 4.14 units. Longer than our first route, so it’s out.

The final route to consider might intuitively seem to be the shortest route. We follow a diagonal line along the outside of the cylinder from Toptown to Downtown. It would effectively be the same thing as if we cut the cylinder open along a line from Toptown straight down and unrolled it, like in my picture below. This route ends up forming the hypotenuse of the triangle formed by the height of the cylinder and half its circumference (half since the towns are diagonally opposite – a whole circumference would put Downtown directly under Toptown). So we use the Pythagorean Theorem to calculate this distance.

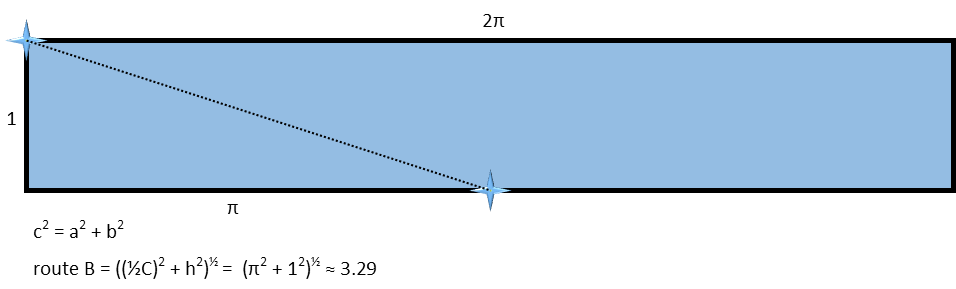
And we see that, even though intuitively that might seem the shortest route since it cuts a diagonal, the fact that it is forced around the circumference of the cylinder-Earth actually makes it longer by a little bit. So our best bet was just to cut across the top disc then straight down (or straight down and then cut across the bottom disc – the resulting distance would be the same).

The key for today’s problem was to make sure to draw the figure to scale, consider all the possible shortest routes, calculate them, and compare.