Math Made Easy: Problem of the Day 52

What is the number problems are fairly popular on the SAT. They test your ability to write equations as well as your number familiarity and reason. The first step is to draw up as many equations as you can based on the information you’re given.

So using the explanation of their arithmetic mean, we write our first equation, labelling our digits A, B, C, and D. But since the value we’re given is four times the arithmetic mean, which is the sum of the numbers divided by their quantity, and there are four digits, the fours will cancel, so 23 is just the sum of the digits.

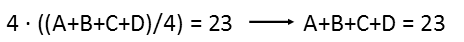
Now we write the equation for the geometry mean, which is the fourth root of their products. The square of that is just the square root. To make it easier, let’s further square both sides so we can see what the product of the four numbers is.

Finally, we see a relation of B to D to A. We can write this as an equation, and then recognize that if B is half of D, then that is also twice A, so D must be four times A. We can then take this relation and plug in the relative value of A for B and D.

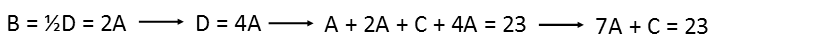
We can do the same for the geometric equation. This one produces something not so pretty, however. There is no integer cube root of 72, so the equation is a little messy. It also won’t make solving this system of equations happy.

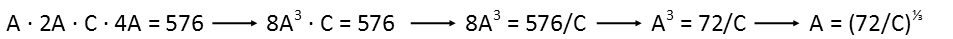
We COULD solve either of our equations for C in terms of A, then substitute that into the other equation, but I can clearly see that’s going to be very messy. So, since we only have 10 digits to try, I’m going to try the plug and play method, where I pick a digit, and plug it into one of the equations to see what I get. I’m going to start at 1, because I know there are very few integers that can actually produce a single digit when double AND quadrupled.

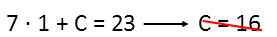
We see that if I pick 1, C has to be 16, and that’s not a single digit, so that’s no good. So let’s try 2.

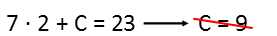
Ah, that gives us a single digit. And in fact, there is no other single-digit integer that’ll work. The next is 3, which when quadrupled is 12 – not a single digit. So now we find B and D from our found value for A.

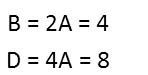
This gives us our number: 2498