Math Made Easy: Problem of the Day 53

This problem must be completed in multiple steps. It is a physics problem, but as far as the physics goes, there are only two equations, and one constant, that one needs to know. They’re readily findable online if you don’t know them, and really not all that hard to remember. It’s certainly all calculable with a high school education.

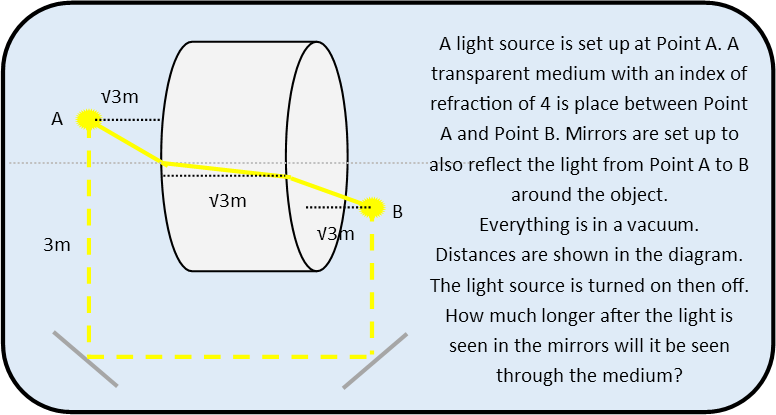
First let’s examine what we need to know to do this. Just what causes refraction? This occurs when light slows down as it enters a new medium. Since light needs to minimize the amount of time it takes to get from point A to point B, and it moves slower in one medium, it alters its route to minimize the amount of time it will take. For light, a straight line is not always the fastest route. Think of the refraction as being caused as the light needing to go uphill – it is frequently faster to take the hill at an angle rather than tromp head on straight up the hill. This means we can calculate the speed of the light in the new medium if we know how it altered its course. This is what the index of refraction tells us, and the formula for it is below. It’s very simple. From that formula, we can solve to get the speed in the new medium.

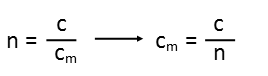
Next we need to figure out HOW that route is changed. Since it’s just a matter of altering route to minimize time, it’s a matter of relating angles to the indices of refraction of the two different materials. So we have the formula below, called Snell’s Law after the scientist who discovered it, which we solve for the sine of the new angle. Note that these angles are in relation to the normal line – an imaginary line we draw perpendicular to the surface of the medium.

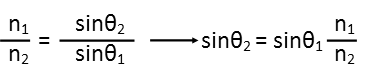
Now we remind ourselves of our indices of refraction. Vacuum is a 1, since that’s the medium through which light travels the fastest.

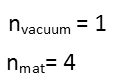
And now we calculate our angle in relation to the normal of the new route of our light inside the medium.

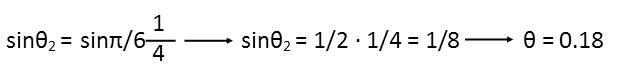
Note I’m keeping everything in radians since it makes our math outside the trigonometric functions easier.

Now that I have those angles, I’m going to redraw my diagram. Always assume that any diagram you are given in a problem is not to scale (and the one in the problem on top of the article isn’t). I will label everything in the diagram, and show you my calculations below it.

Note I drew three right triangles on the diagram. These are going to help me calculate all the distances I need. The first one I will calculate, is the distance the light travels through the medium – this is just the hypotenuse formed by the ray which is the route the light takes, the thickness of the medium, and the base of the triangle formed by those two rays. I have one angle of that triangle – it is the angle between the route the light is taking, and the normal, which is also the width of the medium. I can use the law of sines to find the small side of this triangle. I’ll do that here.

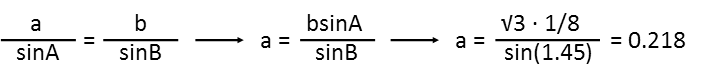
If you’re wondering where I got angle B, it is from subtracting the small angle from &pi/2;, since this is a right triangle. Angle B has to be opposite the side I used, which is the side defined by the width (or normal) of the medium.

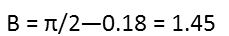
Now I can use the Pythagorean theorem to calculate the length of the route light took through the medium.

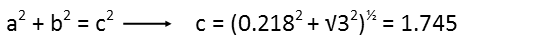
As for the outside triangles, I remembered that they are both 30/60/90 triangles. The sine of 30 degrees is ½. Its cosine is √3/2. The distance the light source is from the medium is the long leg of the triangle, which should be the cosine leg. Since it’s twice the cosine, this tells me the short side is twice the sine, or 1. And that tells me that the hypotenuse is twice that, or 2.

I need to calculate one more length before I’m ready to work on the actual distance of the two routes the light can take, and that’s the distance from the second mirror to Point B. It’s simply the difference between the distance from Point A to the first mirror, and each of the short legs of those three triangles.

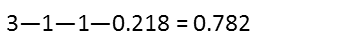
Now I can calculate how long the route via the mirrors is. I just add up the three legs, like so:

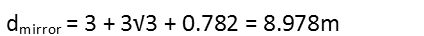
And so the time it takes the light to travel from Point A to the first mirror, then the second, and thence to Point B, is just the mirror route distance divided by the speed of light in a vacuum.

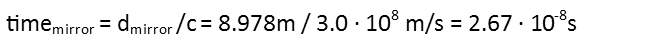
Now is a good time to calculate the speed of light in our medium using the formula we reminded ourselves of previously:

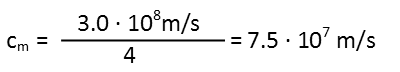
And the time it takes the light to travel from Point A to B through the medium and the intervening space:

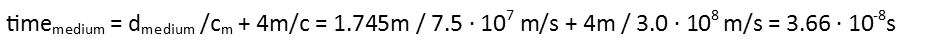
The light got their first taking the long way around via the mirrors. For how much faster, we just subtract the two.

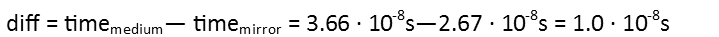
That may seem a very small amount of time, but it’s significant when we’re talking light. It’s measurable. In fact, we can make a shutter fast enough to cut off our view of events. Which brings up the following thought experiment:

Consider causality. The reason speed of light is the fundamental limit of all speeds in our universe is because of the necessity for cause and effect. For any event, the cause MUST precede the effect. But causality goes further than that. Any observer, in any given frame of reference, moving at any given relative velocity, must OBSERVE the cause before the effect. Since light is the universe’s information carrier, that means nothing can go faster than the speed of light – if it did, then we’d end up seeing effects before causes, and we’d never be able to figure out what the heck is going on in our universe. Today’s problem should actually make you question that a little bit.

Consider the shutter I mentioned that can move faster than that gap in time between the light getting to Point B via the mirrors, or via the medium. Consider on shutter over the first mirror, one shutter over the medium. The shutters start out so that the mirror’s shutter is closed, and the mediums mirror is open. The shutter over the mirror does not open until AFTER the cause of our event is done and transmitted to the mirror – so it never reflects a view of the cause, but it does reflect the view of the effect. The medium is exactly the opposite, it shuts the instant the cause is over, and never allows the view of the event to transmit through the medium. So the observer at Point B ends up viewing the Effect in the mirror, and 50 nanoseconds later, the Cause.

So the question is – has causality actually been violated?

I’ll leave that for you to puzzle through. Debate it with your friends.