Math Made Easy: Problem of the Day 54

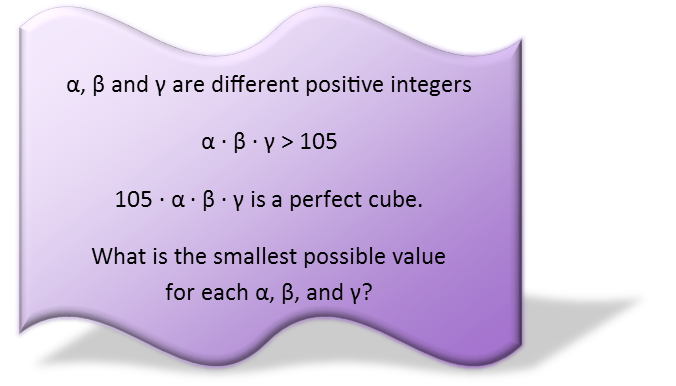
Factoring! It comes up in all sorts of different problems, and it’s definitely the way to go to work through this one. To solve it, we’re going to examine the requirements of the third statement that the product of 105, α, β and γ be a perfect cube. In order for the product of four numbers to be a perfect cube, there must be some common factors. But there’s a limit to those factors – each and every factor must show up exactly three times. So three of the four share each factor of their product. Since we know one and only one of our four numbers to start, let’s factor it. And since we’re looking for the smallest possible values of the other three, we don’t actually care about ALL the factors of 105, just the smallest. A factor tree will be the perfect method for this. We’ll miss some factors (ones that are multiples of the smallest factors of 105), but that’s okay because they’re too big to begin with.

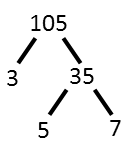
We see that 105 has 3 prime factors, and none of them appear more than once. That’s a good thing, because now we just need to find three numbers that share those three factors. But each factor can only show up two more times. So we’ll factor trees show every combination of 3, 5, and 7, where they are the only factors of their number. And we’ll be careful not to have any of the three appear more than twice.

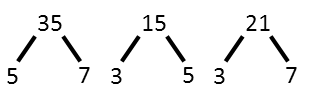
We find our numbers are 15, 21, and 35, and we can assign them to α, β, and γ any way we like. The first requirement is met since they’re all different. Their products clearly are larger than 105, so the second requirement is easily met. To test the third, let’s multiply all four numbers and then take the cube root. I guarantee that cube root is 105, and I know this because we used only factors of 105 to produce the number.

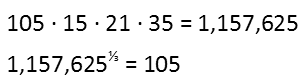
And it is. And if you don’t trust the method we used to find α, β, and γ, you are welcome to play around with numbers and see if you can find any numbers smaller than them that, when multiplied by 105, give a perfect cube. You’ll be looking for a while, and you won’t find anything. But the search can sometimes be worthwhile just to prove it to yourself, as well as to help you work on building up your number familiarity.

Note: it could be argued that another valid solution set is 9, 25, and 49 since those are squares of 3, 5, and 7. This set does work as well, and the product of the set is the same as the product of 15, 21, and 35. However, 9, 25, and 49 have an average value of 27.67 while 15, 21, and 35 have an average value of 23.67, and so is the better solution set.