Math Made Easy: Problem of the Day 55

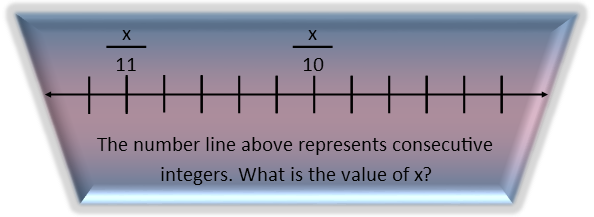
This is another problem that makes use of number familiarity and factoring. We recognize that since the numbers are integers, and that the two numbers on the line are fractions of x, that both of them are factors of x, AND their denominators are factors of x. Also, the difference between them must also be a factor of x. So we must first find their difference. Since they lie on a number line of consecutive integers, we simply count the stops from one to the next.

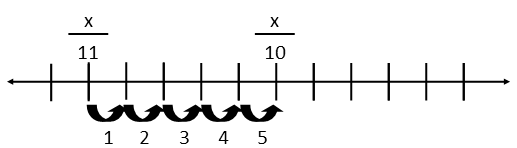
They’re five apart. Now, since, 11, 10, and 5 are all factors of x, we actually don’t need to find x/11 or x/10 – both of those will naturally end up being factors since their denominators will be included in our calculation of x. We do so by simply multiplying the difference and both denominators, as below.

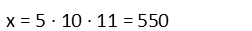
Now that we know x, if we like, we can fill out the number line to confirm we’re right. We find the two numbers we know on the line to be 50 and 55, respectively, since that’s what 550 is when divided by 11 and 10 respectively. Here’s our resulting number line:

That looks like it works. So remember when solving number line problems like this, counting the stops gives you the difference, and from there, the rest is just multiplying. The plug and play assumption method may have worked here, but if you don’t count those stops, you won’t know what number start with, so it’s better to just recognize that the numbers are results of multiplication of factors.