Math Made Easy: Problem of the Day 56

Finding the roots of a function means finding all the places where it equals zero. Composite functions require that you do your math carefully. It’s always best to break it down into steps, and write everything out. Mistakes come from trying to do too many steps at once.

First, we will compose the innermost two functions, f(x) into g(x).and we do that by just replacing all the x’s in g(x) with the entirety of f(x), making sure to surround f(x) with parentheses and treat it like just a single object while we’re going that. Then we just work everything out. Note I expressed the square in a way I could more easily see the FOIL method to expand the quadratic.

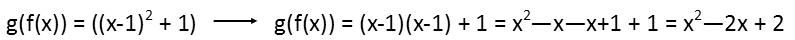
Now we compose the new g(x) into h(x), doing the same thing. This requires a bit more work since we now are squaring a quadratic. Be careful to distribute each and every single term when you expand the new square.

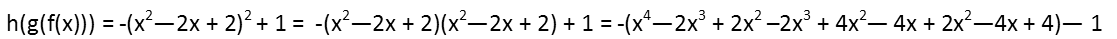
Once we’ve expanded the new h(x), we collect the like terms. Not when I collect all the constants, I brought that -1 inside the parentheses and kept the negative sign outside of the parentheses. Since a negative times a negative is a positive, this had the effect of adding to the constant inside the parentheses. I did this for ease of factoring in our next step.

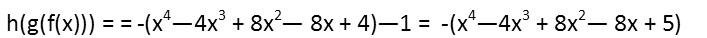
Now we try to factor. It’s not that much different with quartics than with quadratics. All our possible factors come from the constant, which is 5. Five is prime, so it only has two factors – 1 and 5. Since it’s a quartic, each factor will have 3 terms – they’ll in fact be quadratics. The middle term of each factor is going to be dictated by the cube and square terms in the quadratic. We get the following factors for our quartic:

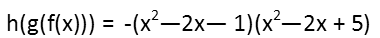
We see that these two terms are not easily factorable. The first requires a negative and positive factor, and there’s no way we can add negative and positive 1 and get negative 2. Likewise, with the other quadratic, no combination of 1 and 5 will give us 2. So we need to make use of the quadratic formula to find our roots.

Let’s remind ourselves of what it looks like:

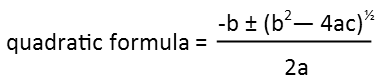
Now it’s just plug and play. We plug in the a, b, and c values from our first quadratic (those are the coefficients of each variable, in alphabetic order, with the constant being c). We find we have two real roots for it.

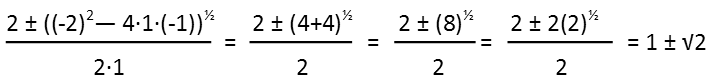
And now we do the same for our second quadratic, finding that it has complex roots.

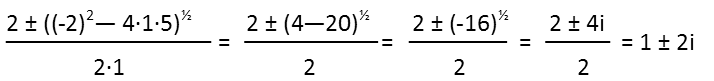
So, as expected from a quartic, we have 4 roots. Two of them are real, and two are complex. We solved the problem by taking it in steps, and writing everything down so we didn’t make mistakes, and made use of the quadratic formula when we could not factor any further.

So, as I keep reminding my students – write everything down, and don’t try to skip steps.