Math Made Easy: Problem of the Day 57

Of the geometry problems we’ve done so far, this is actually one of the easiest ones. Since that top angle is π radians, and the short leg of those right triangles bisect it, their top angle must be π/2 radians (or 60 degrees). That makes the outside triangles one of the easiest right triangles to solve. Remembering our unit circle, we recognize their sides have a relationship of short leg ½, long leg √3/2, hypotenuse 1. Since the long legs are √ 3 meters long, they’re double the measure they’d be for a unit triangle. That means the short leg is twice ½, or 1 meter long, and the hypotenuse must be 2 meters long (though we don’t actually need the measure of the hypotenuses for this problem. Let’s go ahead and redraw the pentagon with these measures marked.

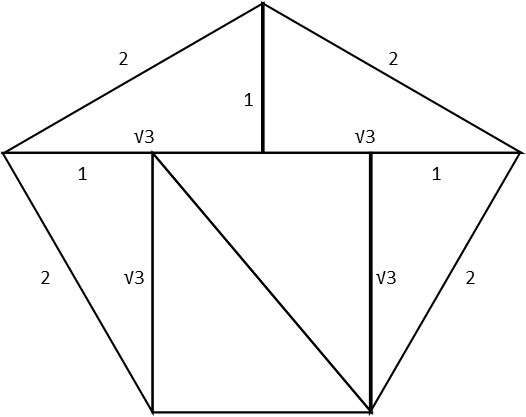
The drawing helps us recognize that, for the two inside triangles, their long leg is the same as the long leg of the outside triangles - √3 meters long. The short leg is made up of two long legs from the outside triangles minus two short legs of the outside triangles (see how the upside down outside triangles short legs abut the long legs of the two top triangles). So we can easily calculate that side.

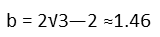
We remind ourselves of the formula for the area of a right triangle (note that it’s a special case of the general formula, where θ is π/2, so sineθ is 1).

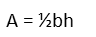
Plugging in the base and height of our outside triangles.

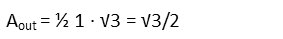
And now the inside triangles.

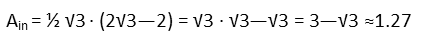
We have two triangles that are red, and both outside triangles, so we just multiple outside triangle area by two to find the area that will be painted red. Since we can only have an integer number of buckets (most stores won’t sell part of a bucket of paint), we need 2 buckets of red paint.

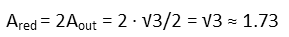
There’s only one silver, and it’s an inside triangle. Again, we cannot buy part of a can of paint, and we need to round up so we don’t run out of paint, so we must by 2 buckets of silver paint.

Finally, we see there are two outside triangles that are red, and one inside triangle. So the black area is just there sum, and we see that when we do that, using the radicals for accuracy instead of decimals, we find the area of black paint is exactly 3 square meters. So we need 3 buckets of black paint.

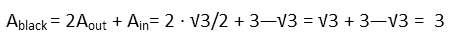
While we could have used trigonometry to solve today’s problem, it was solved using skills entirely accessible to early geometry students. It also required that we remembered at the end that we need whole things (buckets), so we need integers for answers, and those integers must be rounded up so we’d have enough paint to do the job.