Math Made Easy: Problem of the Day 58
Geometry problems are fun, and ones like this help test your ability to think about relationships rather than blindly plugging in numbers. It is good to remind ourselves that there are general formulae for the area of a triangle as well as for the area of any regular polygon.
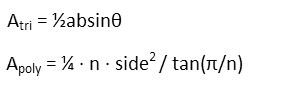
Note that θ in the area for the triangle is the included angle of the two given sides. Since our triangle is an equilateral triangle, which means all sides are equal, all angles are also equal, and so each angle must be π/3 radians (or 60 degrees – we’ll work in radians since it’s better for the math). Each side is the same, so we can plug into our triangle formula to find our triangle’s area in terms of x:
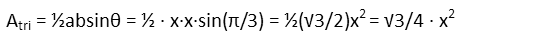
And now we do the same for our hexagon. We don’t need to know the angles, since our formula is done entirely in terms of the number of sides (n and the length of the sides.
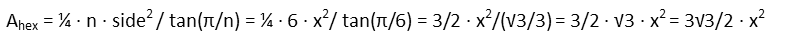
Now that we know the area of each figure, we find how much larger the area of the hexagon is than that of the triangle by simply dividing the larger by the smaller. We can actually ignore the x2 terms in both, since that term is the same, and will cancel out when we divide the two terms. That leaves us with numeric fractions, and we can remember that dividing by anything is the same a multiplying by its reciprocal (a mantra everyone should memorize), so we’ll turn it into a multiplication problem by flipping the divisor. The √3’s cancel and we’re left with an easily simplifyable fraction.
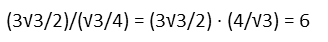
It’s interesting to note that our hexagon is exactly six times larger than our equilateral triangle. This means that, should we have used the technique of dividing the hexagon into triangles to find its area, as I described in Problem of the Day 36, we would have found ourselves dividing it into 6 equilateral triangles. Which would give us a great visual representation of how much larger it is – one we actually could have solved without any computation.
This was a special case, though. As the decagon Problem of the Day 36 showed, we won't always get such a nice, neat separation into equilateral triangles. So I wanted to show the computation as a reminder of how we relate two things in size using differing formulae.
|



