Math Made Easy: Problem of the Day 59

Questions expecting you to handle exponentials are common on the SAT. Mainly because a rather large number of students have a tendency to lose their minds when they see them, and completely forget that they actually do know all the rules to exponents. And problems like this really are just about taking advantage of the rules of exponents to rewrite the expression until it’s in a form that looks more like what you want. And that’s just how we’re going to tackle this one. We want to keep rewriting it until we have an exponent that looks like an algebraic expression, hopefully one very similar to the x² - y² so we can easily just replace it.

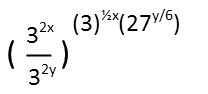
First, we need to get common bases. I see two bases of 3, so I’ll try to relate everything to that. 9 is 3², so I just add a coefficient of 2 to the exponent of 9^x and change the base to three. While I’m at it, I’m going to rewrite that radical as ½ to take advantage of fractional exponential notation to express that, which will allow me to apply all the exponent rules to it.

Next, I see that 27 is 3³, so I’ll give the y in its exponent a coefficient of 3 while changing that base to 3. I see that the fraction 3y/6 simplifies, and I pull the y out of the fraction just to make it a little neater.

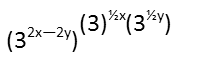
Now I will use the quotient rule to rewrite the fraction in the parenthesis as one exponential term with the fraction’s exponents subtracted bottom from top.

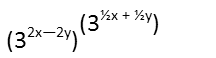
The product rule allows us to rewrite that parenthetical’s exponent as one term with its exponents added together. We’ll write it as two parentheticals multiplied by each other rather than FOILing it out for the moment.

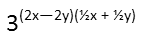
We can factor the two out of the first parenthetical and the ½ out of the second parenthetical. This allows us to see that they readily cancel. So those coefficients just went *poof*. That actually saves us some time.

I don’t need to FOIL out the exponent. I recognize that since the terms in both binomials are identical save the sign in the middle, the exponent is a difference of squares. So I just write it as such. And lo and behold, it is the same difference of squares for which we were given a value. We don’t need to find x or y. We can just replace the exponent with 5 and evaluate.

Our final answer is 243. By not panicking, and just remembering to make use of our exponential rules, we were able to rewrite our expression into a friendlier form that allowed us to readily see we could just swap out the exponent. Remember to do this, and working with exponentials won’t be so bad.