Math Made Easy: Problem of the Day 6

How about another real world problem today? This time let’s talk about lighting. With a little math, and a very basic knowledge of physics, one can determine whether a light bulb will be sufficient to light a room. Brighter paint on the walls will obviously allow dimmer bulbs to be more efficacious due to reflection, but that does make the situation a little more complex. So here’s our setup:

A club promoter is trying to set a nice romantic mood at his venue. He doesn’t want the lights to be too bright – he’d like it just under the light of the full moon - but people need to be able to see. The walls and ceiling are all painted black, and in this one particular room, for some reason or other he wants to use just one bulb to light the entire room. The room is square, 40 meters across, and the ceiling is 10 meters high. The bulb mount is in the center of the ceiling. Currently, the light is a halogen lamp (average luminous efficacy of 20 lumens per watt), and draws 1 watt. For the measure of what people need to see, let’s use the Mythbusters finding where Adam couldn’t make his way around stands with glasses on them when the light dropped below .04 lux. The question is: with this single lamp, will people be able to make their way around the furniture and inevitable glasses on tables at the wall, and is it too bright in the center of the room? Should he replace the bulb? If he needs to, here are his options: a fluorescent lamp with an efficacy of 50 lumens per watt that draws 5 watts, and a mercury vapor lamp with an efficacy of 40 lumens per watt that draws 1 watt.

It’s fortunate the walls are black, because that means we don’t have to worry about reflectivity, which, like I said, makes the whole problem a lot more complex. Let’s also assume that all the bulbs peak at the same place in the spectrum, right in the green, where humans are most sensitive. This removes any need to consider the difference in spectral output of the lights, which also vastly complicates the problem.

So the first thing we need to do, is calculate the luminous output of this light. That’s easy enough. We find the formula for that is I=W x (lm/W). Using this, we find the halogen bulb’s output is 20 lumens.

Now to find how bright that is at the furthest point in the room. To find how far that is from the bulb, we use the Pythagorean Theorem, and recognize that, since the bulb is in the center of the room, it is only 20 meters from the walls at the closest point. So, we have two right triangles to consider. The one we NEED has its base being the distance along the ceiling from the light to the corner, and the leg being the height of the room. And to get that base, we can consider the right triangle whose legs are from the bulb to closest point on one of the walls, and from there to the corner. This gives us a distance from the light to the bottom corner of 30 meters.

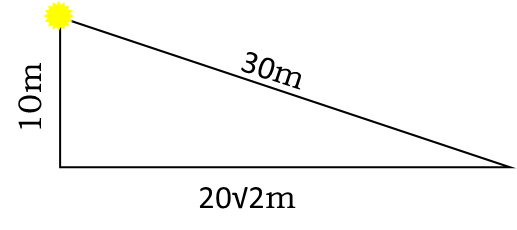
Now to find the actual illuminance at the corner of the room. This follows the inverse square law of light – that the further you are from a light source, the dimmer it is. In fact, the illumination drops off with the square of the distance. So we have use this formula to find the lux at the bottom corner of the room.

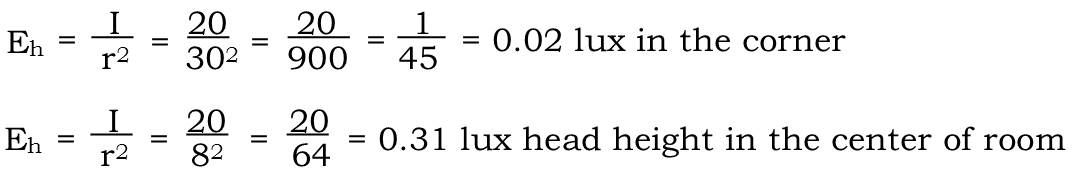
So we see that not only is the 1 watt halogen bulb too dim to sufficiently illuminate the corner of the room, but it doesn’t make quite enough light at head-height in the center of the room (I subtracted 2 meters from the 10 meter height to account the height of a person’s head), directly under it. So let’s look at the other bulbs available to see what works better. First, the fluorescent lamp.

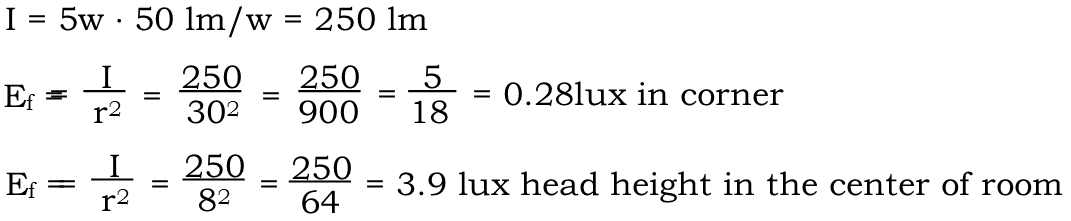
We see that it’s bright enough in the corner, but with an illuminance of 3.9 lux, it's also way too bright in the center of the room. The mercury lamp, however, produces just barely hits our target of 0.04 lux in the corner, and is perfect in the center of the room at 0.63 lux. So our promoter goes with that bulb to light the room.

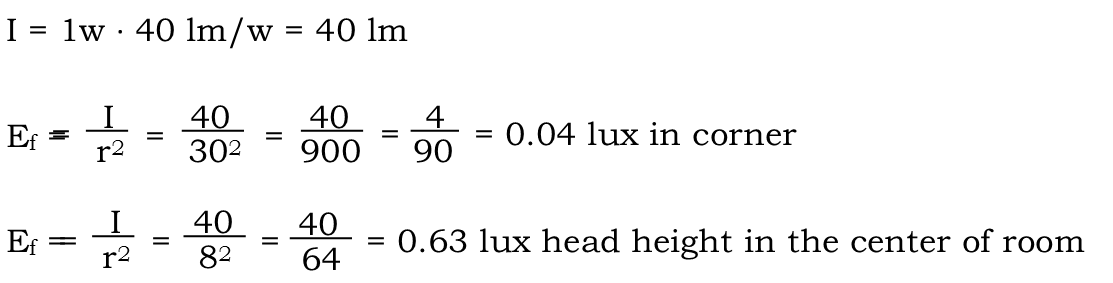
We see that with a little bit of physics, and some math, our promoter was able to decide which bulb would be the best to light his room, without having to make the tedious effort of putting up the ladder and trying one bulb after another until he produced the illumination he wanted. That’s how math can help you in the real world.