Math Made Easy: Problem of the Day 60

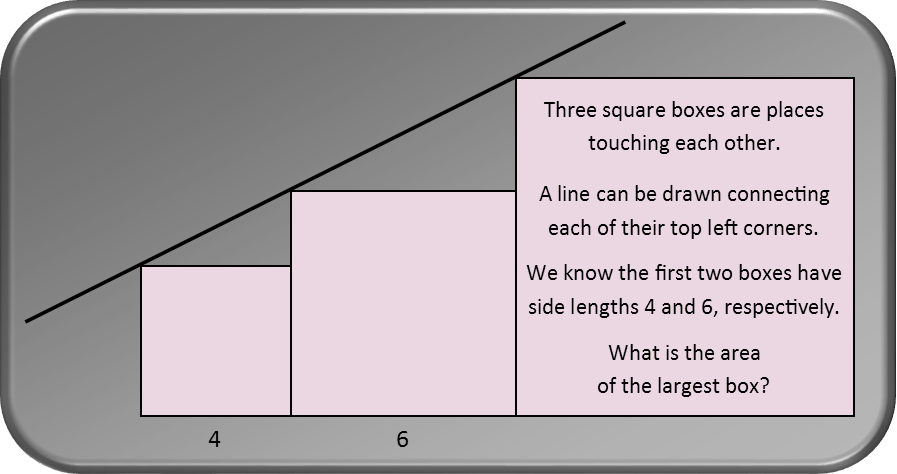
What we have here is a problem in two parts. It is about slopes of lines and areas of squares. To find the area of the largest square, we first need to find the slope of the line connecting the top left corner of each square.

To do so, we can first redraw our figure, placing it on an x-y axis. Since we can pick our frame of reference however we like, it’s convenient to place the origin at the bottom left corner of the smallest square, as I have done below. We then label our points on the x-axis and y-axis accordingly. The y-coordinates correspond exactly to the length of the sides of the squares, as we easily see in the diagram. The x-coordinates start at 0, then the bottom right of the small square has an x-coordinate corresponding to its length. The bottom right of the middle square has an x-coordinate corresponding to its length added to the small squares length, and so on.

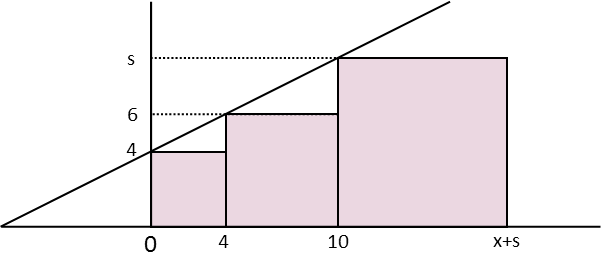
Now that we’ve done that, we can calculate the slope of the line using the ordered pairs at each point. We pick the points at the top left of the little square (0,4) and the top left of the middle square (4,6). We remind ourselves of the equation to calculate the slope of a line from two points.

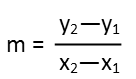
Then we pick our points. I’ll pick (4,6) as point 2 and (0,4) as point 1. It doesn’t really matter which is which, though – the slope will come out the same either way. We plug the respective x and y values into our formula, and simplify, finding the line’s slope to be ½.

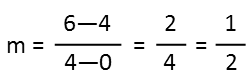
We can now calculate the y-coordinate in the top left point in the big square. We remind ourselves of the slope-intercept form equation of a line:

We note that the y-intercept is the point where the line crosses the y-axis, which, due to the convenience of how we selected our origin, is the top left corner of the little square, or 4. Our m is the slope, or ½, and b is our y-intercept, or 4. We plug those in, and then use the x-coordinate of the top left corner of the big square, which we already know to be 10 since it shares that with the x-coordinates of the right-hand side of the middle square. Doing this, we find the y coordinate of the top left corner of our big square to be 9.

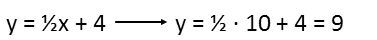
This means it has a side-length of 9. So we can easily calculate its area, since the area of a square is just the square of its side lengths.

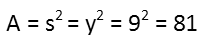
Recognizing what your problems are really about is key to solving them. This one was mostly about the slope of a line. The area of squares was just secondary, and really only necessary to find our final answer. So don’t be blinded by trying to find the final answer to the point that you don’t see the real substance of the problem.