Math Made Easy: Problem of the Day 62

There are a few ways you can solve a system of equations. Graphing, substitution, elimination, and conversion to matrix form will all work. For today, I’m going to use the elimination method to solve this system.

For the elimination method, we must remember that we are trying to add or subtract one equation from another with the aim of eliminating variables, making them go away. We may need to multiply one or more equations by a constant to help us achieve this aim. So we first start by looking for two of the equations where we could easily eliminate a variable by addition or subtraction. I see that both equations on the right have a variable y with the same magnitude and sign. So I can subtract one from the other to eliminate that variable.

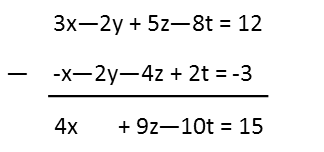
Next I will use the two equations on the left to eliminate the y variable. I see that they have the same magnitude, but different signs, so I can eliminate the variable by adding those two equations.

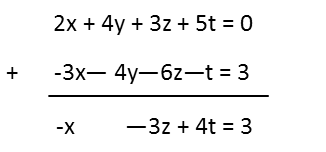
I then take the resulting two equations and place them one above the others so I can more easily compare them. I see that if I multiply the top equation by 4, I can add the two equations to eliminate the variable x. I could also multiply the top equation by 3 and eliminate the variable z, but I’ll go with getting rid of x.

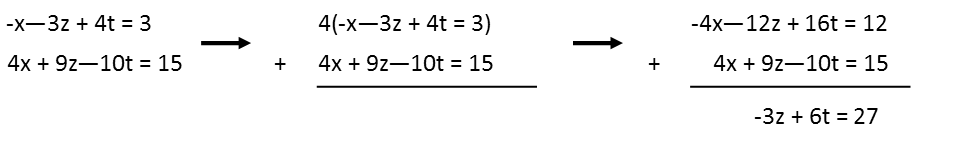
Once I’ve done that, I have an equation with only two variables. I want to solve in for one in terms of the other. z has the smaller coefficient, so I’ll solve for it in terms of y.

I’ll take my new expression for z and replace that variable with the expression in my original four equations.

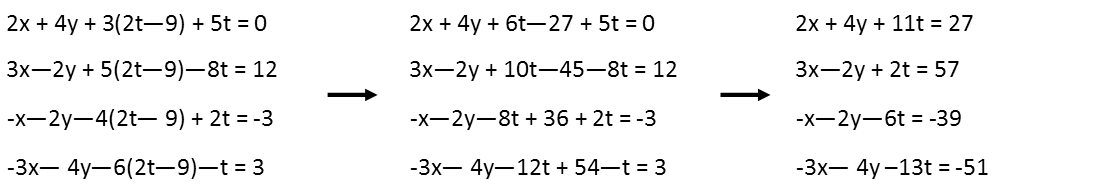
I’ll now repeat the elimination process. This time I see I can eliminate x if I add the second and fourth equations.

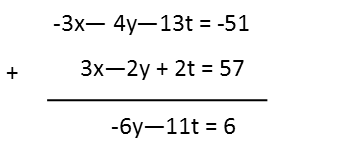
Now with the other two equations, I can also eliminate x by adding if I first multiply the bottom equation by 2.

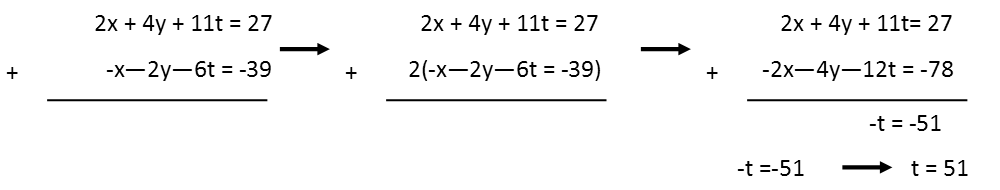
It’s actually quite convenient that the variable y also eliminated, because I now know exactly what the variable t is. I do not have to do any more elimination steps. Now I can start solving for the other variables. I’ll first find y by plugging my value for t into the expression I found that involves only those two variables.

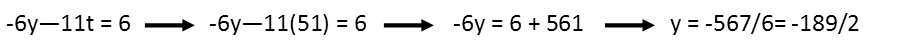
Then I can solve for z by using the expression that involves only it and t:

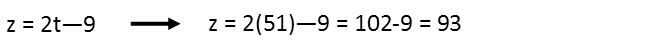
Now that I have every variable but x, I pick one of the original equations and plug in all the values I have, and solve for x. Since I can pick any of the equations, I’ll pick the top right one since it’s got the smallest coefficient of x, which should make solving for it a bit easier.

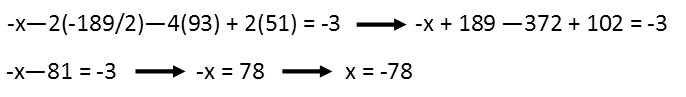
Finally, never trust yourself. Always check your math. With systems of equations, we can do so by plugging in our solution set to each of the remaining equations. If they check out, we’re golden!

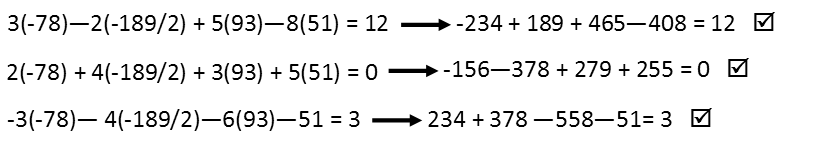
They do, so our solution set is (-78,-189/2,93,51).

It’s important to write down ALL your work, and to check your work when you’re done. When I originally worked this problem through, I made a sign error early on, and didn’t catch it until I got to the check my work step. When I did the check, I got horrible values on the left side of the equations that absolutely did not match the right side. But, because I’d written down my work, I was able to go back through it and find where I made my error. It was a simple sign error that made my equation for z turn into z = -2t + 9. Which of course changed everything I did after that step. If I hadn’t written down everything I did, I wouldn’t have been able to find the error, and I would have had to throw out almost an hour’s worth of work and start all over. I cannot stress enough the importance of writing down every simple step in your math, and always, always, always check your work.