Math Made Easy: Problem of the Day 63

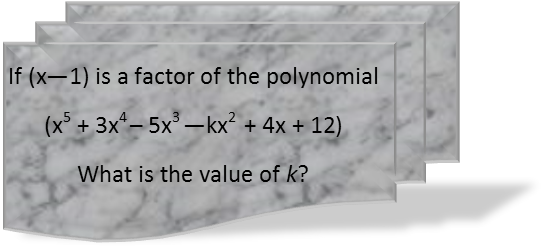
Not all factoring problems are created equally. This problem, while about factoring, becomes a bit more difficult if you try to approach it as a traditional factoring problem. Trying to find all the factors of this polynomial, when you don’t know one of the coefficients, will be a tiresome and lengthy process with lots of dead ends if you go about it the wrong way.

One tool almost all my students learn in their second year algebra course is also one that most of them fail to recognize can help them find factors. Even though, when they learn the tool, they are taught to use it to test to see if something is a factor of a polynomial. That tool is synthetic division of polynomials. And it’s the perfect tool for this problem, because we can use our knowledge of how it works, and backsolving, to find k.

So let’s set this up as a synthetic division problem. We set up a 3-row table. On the top row, starting in essentially the second cell, we write just the coefficients of the polynomial, including their sign, in order, one to a cell. The first cell of the middle row gets the zero of the factor. That is, if we set the factor equal to zero, and solve for the variable, what do we get? Note that the zero always has the opposite sign of the constant in the factor.

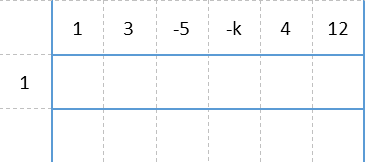
The way synthetic division works from here, is we drop the first coefficient all the way to the bottom. Then we multiply the zero (that number that's out to the left on its own) times that, placing the product under the next coefficient. We add those two numbers. Then we repeat the process. It forms a zigzag pattern, which I’ve illustrated below. With what we have, let’s complete the pattern until we get to -k.

Once we cannot continue at -k, we need to plan how we’re going to find k. We do that by backsolving. We know that, for something to be a factor, there must be no remainder when we finish the synthetic division. This means the very last number in our table must be a 0. So we’ll place a zero in the third row directly under the 12. Then we’ll start backsolving – what do we need to add to 12 to get 0? That number MUST be -12. We fill that in under the 12, and also carry it to its spot in the bottom row directly under the 4, and determine what we must add to 4 to get that, and so on, until we’ve filled out every spot in the bottom two rows.

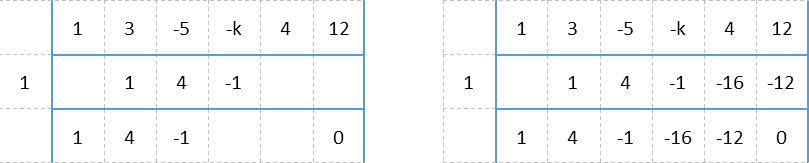
We now see that we need to determine what we need to add to -1 to get -16. Only one number will work, and that is -15. So we have found -k. Since we were asking what k is instead, our answer is 15.

Remember the tools available to you, and how you can take advantage of them to solve your problem. Backsolving is a great way to find some difficult problems that would otherwise require a lot of trial and error headache.

For some added challenge, go ahead and find the remaining factors of the polynomial. You can continue to use synthetic division to find them.