Math Made Easy: Problem of the Day 64

This may seem harder than some of our previous painter problems, but it really isn’t. We could try to set up triangles to determine our areas, and figure out arc segments, but there’s a much faster and easier way to do it. And that way is to recognize this is all about conics, and equations of that ellipse. So let’s consider the ellipse in the equation given.

It’s not in the form we want an equation for an ellipse to be in. We need to do some algebra to put it in that form. Let’s remind ourselves of the general form of the equation for an ellipse, using a horizontal ellipse to do so. Don’t worry about whether this one is horizontal or vertical yet – the algebra will play it out and show us which in the end.

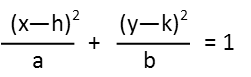
The first thing we’re going to want to do to make the equation we were given look like that, is to group the x’s and y’s, and move the constant to the right-hand side of the equation. Let’s also factor a 4 out of both x’s, and a 9 out of both y’s while we’re at it. In preparation for a next step, I’m going to insert a question mark into each grouping. You’ll see why in a moment.

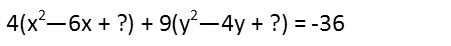
So that question mark. I put it there because we need to complete the square now. This’ll give us the ability to create two quadratics which are perfect squares, which we can then factor, as we see in the ellipse form there is a factored perfect square on the top of each fraction. To complete the square, we remind ourselves that the question mark is just:

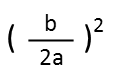
Where b and a are just the coefficient of the the first two terms in the quadratic in alphabetic order. We also have to remember that when we complete the square, we’re adding to the left-hand side of the equation. And whatever we add to it, we add to the right. Since we factored a 4 out of the x group and a 9 out of the y group, we need to multiply what we add to each group by that amount, and add that to the right-hand side as we go, like so:

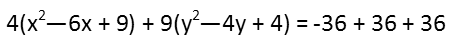
Consolidating the constant on the right-hand side:

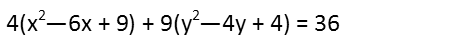
And now factoring the x and y groups:

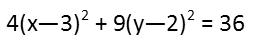
We now divide both sides by 36 so we can get a 1 on the right-hand side, like we need. This also turns the left-hand side into two fractions, which we also need.

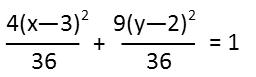
Finally, simplifying those fractions, we get the desired ellipse form:

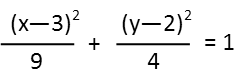
We now see that our ellipse is a horizontal ellipse (since the big denominator is under the x) whose major axis has a radius 3 (the square root of the big denominator), and semi-major axis has a radius of 2 (the square root of the small denominator). I call them radii to remind us that this is the distance from the center of the ellipse to the vertices and co-vertices, respectively. This also helps us relate the ellipse to the circle better. Since the ellipse is inside the circle, and their edges touch, the circle’s radius MUST be the same as that of the major axis of the ellipse. This is because a circle is just a special case of an ellipse. We will also see that in the similarity of their area equations.

That means we’re now ready to calculate the areas of the paint. The pale blue paint fills the entirety of the ellipse, so the area it covers is just that of the area of an ellipse. The equation for that is quite simple. Note that a and b are the radii of the major and semi-major axis of the ellipse.

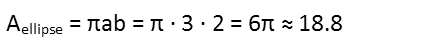
The pale yellow paint fills the area of the circle not covered by the ellipse. So we subtract the ellipse’s area from that of the circle.

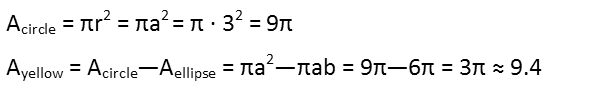
And reminding ourselves that the painter can’t buy partial buckets of paint, we round up for both. He needs 19 buckets of pale blue paint and 10 of pale yellow.

As I said at the start, this problem *could* have been solved with triangles and arc segments, but that way would have been MUCH more complicated. If the painter had just been given the lengths of the axes of the ellipse, it would have been very simple, as well. Normally, that’s what he would have been given, but I wanted to do it as an equation for a little bit of added difficulty. It’s also useful to be able to remember the equations of geometric shapes like this for scaling purposes – using that equation, he can scale the ellipse and circle to whatever he likes without changing their proportions.