Math Made Easy: Problem of the Day 65

I’ve largely been avoiding calculus in the problems of the day, but I decided to use a calculus approach for today’s problem, as it’s simply the fastest way to do it. We could remember our kinematic equations, which I’ve discussed before in Problem of the Day 10, but we can still do this problem if we can’t remember them. We just have to derive our own equation of motion, and that’s the very reason Newton and Leibniz developed calculus.

To get the sphere’s volume after any given time, we recognize it is dependent on the radius of the sphere. So let us contemplate a point x on the surface of the sphere. Let’s also conveniently place axes with the origin at the center of the sphere, and point x exactly on the x axis. The distance from our point to the origin is the same as its coordinate. This means that the coordinate point x is exactly the radius of the sphere. So if we can express its coordinate as a function of time, we can easily find the radius of the sphere at any given time. So let’s look at our given information.

For an object with constant velocity, its distance travelled, or position relative to the origin, is equal to its velocity times the amount of time travelled. So we know that’ll be the first part of our position equation. But, this object is not travelling at a constant velocity. It is slowing down. Since there’s no such thing as deceleration – there is only acceleration in the opposite direction, or negative acceleration – we recognize that the point is constantly accelerating in the direction opposite its motion. We can thus describe the effect this negative acceleration has on its velocity as a function a(t).

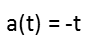
Note that I didn’t write the 1 from its slowing down by 1 m/s². In calculus and equations of motion, it turns out that position, velocity, and acceleration are intimately connected. Velocity is the derivative of position, and acceleration is the derivative of velocity with respect to time. Since I’ve expressed acceleration with respect to time, we can take the anti-derivative of that expression to find the velocity change as a function of position with respect to time. We also call the anti-derivative the integral. Really this just means doing a derivative backwards. Note that when we take an indefinite integral (one that’s not being evaluated over a given range), we have to add an unknown constant at the end, since the derivative of a constant is zero (it vanishes when we do the derivative forwards, so doing it backwards we have to account for that vanishing constant).

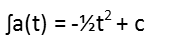
What could that constant be? We’re talking about crafting a position equation, and we’re actually given a constant in our information – the initial radius of the sphere, which is the initial position of our point on the sphere’s surface.

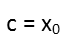
With our integral of acceleration, and our notion of how we’re going to express position based on the initial velocity, we write our position equation. It’s just going to be the sum of what the position would be if that initial velocity were constant, and the velocity change from the acceleration of the point (plus the initial position of the point, or the constant in the integral).

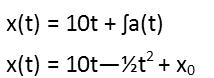
If you check the kinematic equations from Problem of the Day 10, you’ll see this looks an awful lot like the position equation from them. That’s because it was derived the same way.

Now to find the maximum volume of the sphere. We recognize that the maximum volume of the sphere will be the point at which the radius is at its maximum. We could find this by trying to find when the velocity equals zero. OR we could use calculus again to find the maximum of the position equation. We do this by taking the derivative of the position equation, and setting that equal to zero. This works because the derivative represents the rate of change of the equation. Rate of change can be represented as the slope of a line. When that line is horizontal, the velocity at the point where its about to start getting smaller. A horizontal line has a slope of zero.

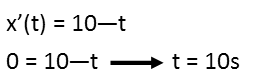
We see this happens after 10 seconds. Now that we’ve found the point in time where the velocity is zero, and the sphere is about to start collapsing (if the acceleration remains the same), we can plug that time into our position equation to find the actual radius of the sphere after 10 seconds.

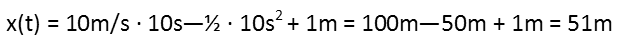
The sphere’s maximum radius is 51 meters. Reminding ourselves of the equation for the volume of a sphere, we plug this radius into that and solve. Note I also converted from cubic meters to liters. There are 1000 liters in a cubic meter. Also note that I used scientific notation to avoid writing all those extra zeroes.

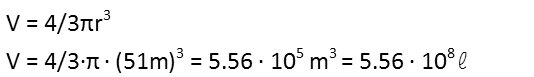
The problem could be done without calculus, if you remember the kinematic equations. The hardest part would be finding the maximum radius of the sphere, which you could do by using the third kinematic equation (without the sine function) and setting it equal to zero. The approach I used is a little easier, and can be done without memorization of formulae, except for the volume of a sphere (and even that you could derive with calculus if you can’t remember it). I didn’t explain how to do a derivative, quite, but that would be for one of my regular Math Made Easy articles, not for a Problem of the Day.