Math Made Easy: Problem of the Day 67

Subtracted area or volume problems are classic problems on standardized tests. They assess your ability to visualize the geometry of the situation, and relate portions of one figure to another. You are frequently asked to solve them with very little information. In this case, we are only given two quantities, but that is more than enough to solve the problem with the relationships given.

So let’s first redraw a diagram of what’s going on, and label everything we know. Since we know the radius of the cone is one third its height, we know that radius must be 3cm, so we can label that accordingly. Note that our diagram doesn’t have to be 100% accurate to scale – and it rarely will be unless we’re an astounding artist. What matters is that we label it correctly and it’s sufficient that we can see the relationships we need to see. I actually drew this one intentionally out of scale just to illustrate that point.

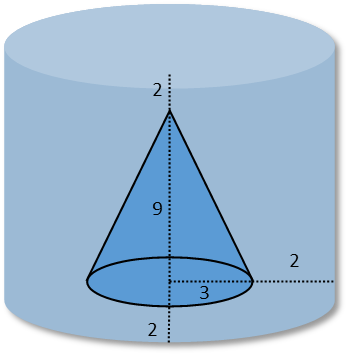
Now that we’ve done that, we can recognize that the amount of water the bottle can hold isn’t the entirety of the volume of the bottle. The gel container occupies part of that volume, so that means there’s that much less water in the bottle. So we can take a moment to remind ourselves that the volume of water in the bottle can be found by subtracting the cone’s volume from the bottle’s volume.

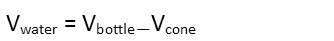
Let’s calculate the cone’s volume first. We remind ourselves of the formula for the volume of the cone.

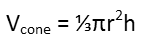
Then we plug in the height and radius, which we know, and solve. It’s convenient that the ⅓ and the 9 simplify to 3 before we process any exponents. That allows us to rewrite the equation with 3³ instead of 3² times 9. Let’s leave it as 27πcm³ for the moment for more accurate results later.

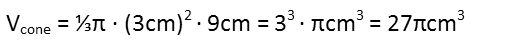
Now to remind ourselves of the formula for the volume of a cylinder for the bottle.

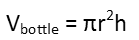
We can then reason out the radius and height of the bottle. Since the extremities of the cone are all 2cm away from the walls of the bottle, we can reason that the radius of the bottle is 2cm bigger than the radius of the cone, or 5cm. That’s because the circumference of the circle marks one extremity of the cone. Its vertex is the other, which, combined with the base being the circumference of the cone, tells us that the bottom of the cone is 2cm from the bottom of the can, and the vertex of the cone 2cm from its top. So the height of the can is 2 + 2 = 4cm more than the height of the cone, or 13cm.

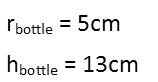
So plugging in the height and radius of the bottle to its volume formula, we get 325πcm³.

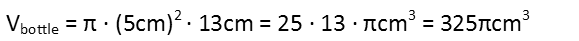
Finally, we subtract the two, and approximate our volume of water. It turns out or bottle holds a little under a liter of water, which isn’t bad.

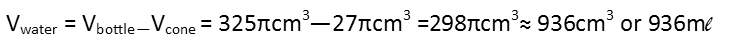
By redrawing our diagram, labelling it correctly, and reasoning out the situation, we turned this into a pretty easy problem.