Math Made Easy: Problem of the Day 68

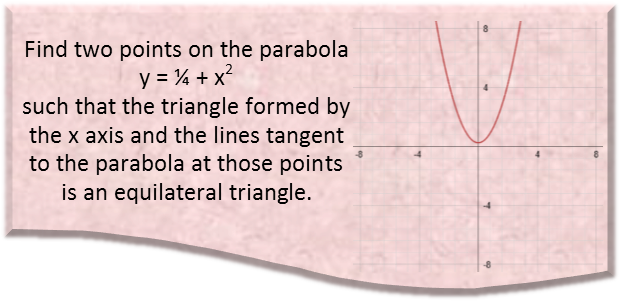
It’s time for some more calculus! But don’t get too worried – the calculus needed for this problem is pretty simple. But before we get to the calculus, let’s first consider the geometry and trigonometry of the situation.

In order for those tangent lines to form an equilateral triangle with the x-axis, they must form angles of measure π/3 radians with the x-axis. We then consider that the slope of a line is rise over run. This is convenient for us, because the angle these lines form with the x-axis has a rise-over run to any point on the line equal to the tangent of the angle (just picture it on the unit circle – tangent is y/x on the unit circle, which is rise over run). Recognizing this, we calculate what the slope of these lines must be:

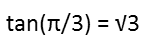
We also recognize that, because there are two tangent lines, in different quadrants, and the only difference in tangent in different quadrants its sign, the two lines have basically the same slope, just with differing signs. Their slopes are ± √3.

Now enters the calculus. The lines tangent to a parabola represent the rate of change of the parabola. The rate of change of any function is its derivative. So if we take the derivative of our parabola’s equation, we’ll find the expression for the slope of its tangent lines at any given point. To take the derivative, we use the power rule for derivatives – bring the exponent down so it becomes the coefficient (multiplying by any existing coefficient), and subtract one from the exponent. This effectively makes the derivative of any constant zero. So our derivative looks like this:

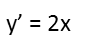
Recognizing that we already know the slope, we set the derivative equal to that to find the x-coordinate for our tangent points. Note I did it for one, since the only difference in the slopes is a sign. That means the only difference in the x-coordinates of the tangent points is the sign.

With the x-coordinate of the tangent points found, we plug that into the parabola’s equation, and find the y-coordinate. Again, since the only difference in the x-coordinate is the sign, I only need to do it once. The y-coordinate will be the same for both points since the x-coordinate’s sign will vanish when squared.

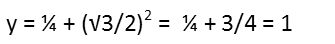
This gives us the following two points for our tangent lines:

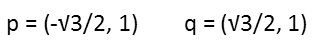
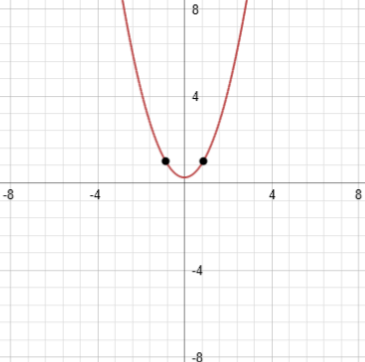
Plotting them, we find them directly on the parabola, as they should be.

We’re basically done with the problem now. But if we’re curious, or don’t trust our math to this point, we can go ahead and calculate the actual tangent lines. We start with the slope-intercept form of their equations, recognizing that we know the slopes, but not their y-intercepts.

To find the y-intercepts, we plug the coordinates in for the points we know are on those lines, and solve for b (the y-intercept).

We see that they’re the same y-intercepts, which shouldn’t be surprising. In fact, it’s what we should have expected – the parabola is not shifted horizontally, so the lines should meet on the y-axis.

Plugging the y-intercept in, our tangent line equations are as follows:

Let’s plot everything we have now!

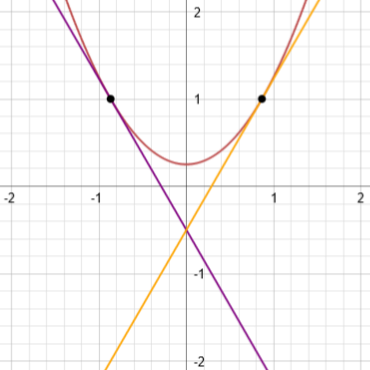
We can see the triangle the tangent lines form with the x-axis now. It’s below the x-axis, and is very small, but it is clearly an equilateral triangle, as we wanted. Excellent! Note I zoomed in on the graph for this so we could see the triangle better.

Without calculus, this actually would have been quite a difficult problem to solve. Knowledge of the derivative can really make your life easier, and it’s really not that hard to do.