Math Made Easy: Problem of the Day 69

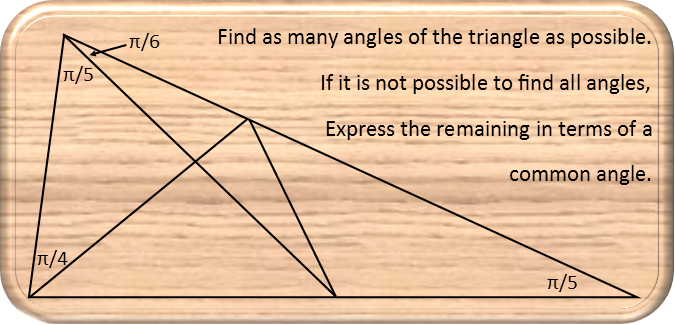
Problems where you are expected to solve many things in one can seem daunting. But if we just break them down, and start tackling it one piece at a time, as we see the pieces we know how to solve, they will become much more manageable. We also must recognize, that when solving problems involving geometry, we must not trust our eyes. Even when the diagrams provided are drawn to scale, and that aren’t always (as this one is intentionally drawn out of scale), our eyes can deceive us. We must rely on sound geometric and mathematic principles to solve them.

First, let’s draw a new diagram, and label all the unknown angles with a variable. If you’d like, you can try rescaling it, but this one might be difficult to figure out what shape the triangle is in its true scale, so I’m just going to leave it as it is.

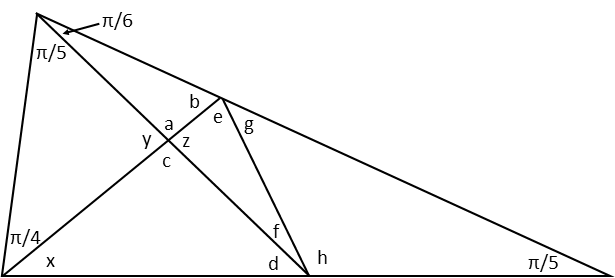
Now let’s solve one angle at a time. I’m going to start with the angle I labelled x because I see it can be found by the largest triangle, whose angle are the right-hand angle of π/5; the sum of the top two angles, and the sum of the bottom left angles (π/4 and x). Recognizing that the sum of all angles of a triangle in radians is π, we know the sum of those angles must also be π. I’m also going to use a trick I teach a lot of my students – since π is going to be in the numerator of every angle measure, we can treat it like a thing. A thing that I can remove entirely and ignore until I’m done calculating each angle. This allows me to treat each angle as a simple fraction. Which is actually part of why radians are so useful. So now I just set the sum of each triangle to 1, with the angles of each triangle adding up to that.

So for x, we have:

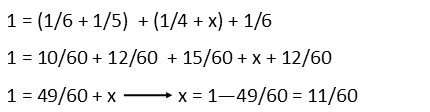
Solving for y the same way, we get:

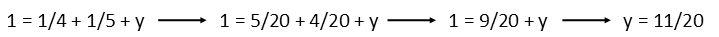
Angle a is simpler. It’s supplementary to y, so their sum must be π, or 1 for my simplified equations:

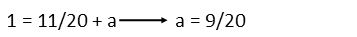
For angle b, we use the triangle comprising it, a, and π/6:

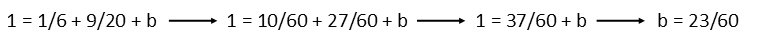
Angle c is vertical to angle a, so they are congruent. Likewise, z is congruent to y, as they are also vertical angles. This allows us to find d using the triangle comprised of angles x, c, and d.

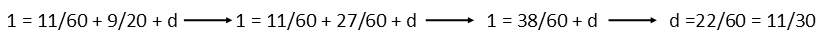
Now we might be stuck. We have 4 angles remaining, belonging to two separate triangles. Neither of those triangles has two known angles at this point. Those 4 angles also belong to 2 different groups of supplementary angles. Each of those groups is made up of 3 angles, two of which are unknown. So we can’t solve them directly, but maybe we can set up a system of equations. This will give us 4 equations each with two unknowns. This *might* be enough to solve for the angles, UNLESS the system ends up being circular. This one turns out to be circular, so it’s not actually solvable – if you try the substitution method, you’ll end up following a circle where you completely cancel a variable and prove a fraction equals itself (go ahead and try it). But we can pick one of the angles, and choose to solve for all the other angles in terms of it. So I’ll pick h, and express angles e, f, and g in terms of h. Note that for e, I have to find another variable in terms of h, and substitute that for the variable in one of the equations involving e. I’ll pick f for that. We end up with the following:

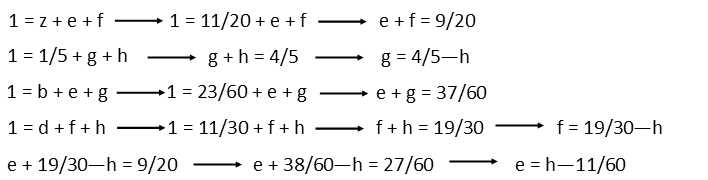
So let’s label our triangle with what we found for all the angles.

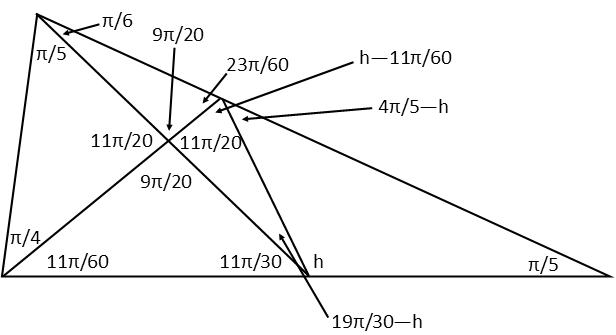
And we’ve done as much as we can with this triangle. Most of the angles we were able to find. But to find the remaining four angles, we’d need one more piece of information – just one more angle from one of the two last triangles. If we’d had that from the start, we could have found every single angle in the diagram. And we came to this conclusion by breaking the problem down into simple steps, and solving for one angle at a time.