Math Made Easy: Problem of the Day 7

Today’s problem is solvable without any computation. Just by using your reason, and remembering properties of triangles, one can determine the answer without resorting to any formulae. I will, however, go through the formulae and computation needed to solve it just to demonstrate, and prove the property.

Observe the triangle drawn. Note that it is not to scale. We do not know any of the angles, or two of the sides. All we know is that one side has a length of 10, and that the triangle is isosceles. This means the two other sides are congruent to each other, or have equal length. What is the smallest possible integer length of those sides?

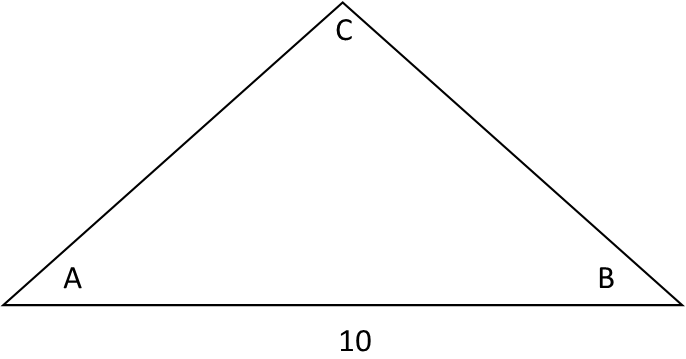
Like I said, all we have to do here is remember some properties of isosceles triangles. That being that the third side can never be twice the length of, or more than the two congruent sides. Knowing this, and remembering that an integer is any whole number, we can reason that the shortest integer length the other two sides can have is 6. Now let’s prove it.

To prove it, I’m going to use the law of cosines. It is a more general case of the Pythagorean Theorem that applies to all triangles. It looks like this (note that lower case letter represent the lengths of sides, and capital letters represent the measure of angles):

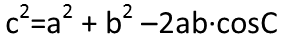
In our triangle, a=b, since it’s isosceles. This is great, because it gives us an equation with only one unknown, that being angle C. But before I start plugging numbers in willy-nilly, I’m going to use my algebra to solve for angle C, since that’s a much easier approach.

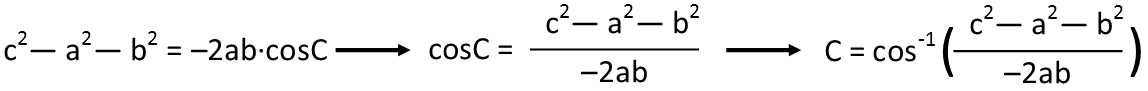
Now that I’ve done that, let’s plug in our numbers. Since we’re trying to prove that the third side can’t be twice or more the two congruent sides, I’ll plug in 5 for those two sides. I’m also going to work in Radians, since it’s a much better unit of measure than degrees (radians is a derived measure while degrees is arbitrary). And a remember: that negative exponent over the cosine function means use the inverse cosine function on a calculator – in other words, what angle returns a cosine of whatever junk you get inside the parentheses.

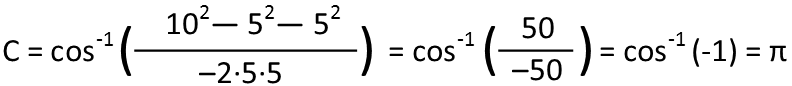
We see that we got an angle of π radians. For those not versed in radians, that’s 180 degrees, which is a straight line. In other words, we don’t have a triangle any more. That’s no good. So let’s give those sides a length of 6 and check that just to make it works.

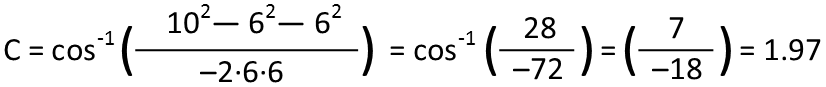
We get 1.97 radians, or about 113 degrees, which makes for a perfectly viable triangle.

So we see that we were able to solve this problem with no computation! But a little bit did help to confirm our answer. As far as the upper limit for those two congruent sides, there is none. If you’d like to prove it to yourself, just play around with some large values for them in the law of cosines. You’ll find that no matter how big you make them, you still get a valid angle. A tiny one with really large sides, but a valid one nonetheless.